题目内容
3.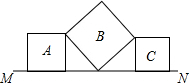 如图,在直线MN上有三个正方形A、B、C,若正方形A和正方形C的面积分别为16和20,则正方形B的面积为( )
如图,在直线MN上有三个正方形A、B、C,若正方形A和正方形C的面积分别为16和20,则正方形B的面积为( )| A. | 24 | B. | 36 | C. | 40 | D. | 48 |
分析 根据已知及全等三角形的判定可得到△QWF≌△FDE,求出QF的长,即可得出答案.
解答 解: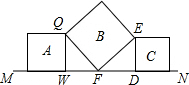
由于A、B、C都是正方形,所以QF=EF,∠QFE=90°,∠QWF=∠FDE=90°,
∵∠WQF+∠QFW=∠QFW+∠EFD=90°,即∠WQF=∠EFD,
在△QWF和△FDE中,
$\left\{\begin{array}{l}{∠WQF=∠EFD}\\{∠QWF=∠FDE}\\{QF=EF}\end{array}\right.$,
∴△QWF≌△FDE(AAS),
∴QW=FD,WF=DE,
∵正方形A和正方形C的面积分别为16和20,
∴QW2=16,DE2=20,
∴WF2=DE2=20,
在Rt△QWF中,由勾股定理得:QF2=QW2+WF2=16+20=36,
∴正方形B的面积为36,
故选B.
点评 此题主要考查对全等三角形和勾股定理的综合运用,关键是证明△QWF≌△FDE.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
13.若a>b,则下列结论正确的是( )
| A. | a+2<b+2 | B. | a-5<b-5 | C. | $\frac{a}{3}$<$\frac{b}{3}$ | D. | 3a>3b |
14. 如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上,若∠1=25°,那么∠2的度数是( )
如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上,若∠1=25°,那么∠2的度数是( )
 如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上,若∠1=25°,那么∠2的度数是( )
如图,把一块含有45°的直角三角形的两个顶点放在直尺的对边上,若∠1=25°,那么∠2的度数是( )| A. | 35° | B. | 30° | C. | 25° | D. | 20° |
8. 如图,△ABD≌△ACD,∠BAD=40°,则∠BAC=( )
如图,△ABD≌△ACD,∠BAD=40°,则∠BAC=( )
 如图,△ABD≌△ACD,∠BAD=40°,则∠BAC=( )
如图,△ABD≌△ACD,∠BAD=40°,则∠BAC=( )| A. | 20° | B. | 40° | C. | 80° | D. | 不确定 |
15.在同一平面上,正方形ABCD的四个顶点到直线l的距离只取两个值,其中一个值是另一个值的2倍,这样的直线有( )
| A. | 16条 | B. | 12条 | C. | 8条 | D. | 4条 |
12.下列不是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}2x+9y=0\\ x+y=0\end{array}\right.$ | B. | 3x=4y=1 | C. | $\left\{\begin{array}{l}\frac{1}{x}-2y=2\\ x=1\end{array}\right.$ | D. | $\left\{\begin{array}{l}x=3\\ y=2\end{array}\right.$ |
13.手机给我们带来方便的同时也给我们带来辐射,手机在刚拨出号码时对人体的辐射最大,其实在我们身处的自然环境中,每人一年接受的宇宙射线及天然辐射照射量约为3100微西弗(1西弗等于1000毫西弗,1毫西弗等于1000微西弗),用科学记数法可表示为( )
| A. | 3.1×106西弗 | B. | 3.1×103西弗 | C. | 3.1×10-3西弗 | D. | 3.1×10-6西弗 |




