题目内容
6．解下列不等式组：$\left\{\begin{array}{l}2x-5＜3x\\ \frac{x-2}{2}＞\frac{x}{3}\end{array}\right.$．分析 分别解出两个不等式，进而得出不等式组的解集即可．
解答 解：$\left\{\begin{array}{l}{2x-5＜3x①}\\{\frac{x-2}{2}＞\frac{x}{3}②}\end{array}\right.$，
解不等式①得：x＞-5；
解不等式②得：x＞6；
所以不等式组的解集为：x＞6．
点评 此题考查一元一次不等式组的解法，关键是根据不等式组的解集取法解答．
练习册系列答案
相关题目
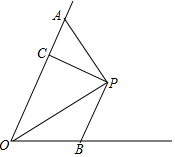已知：如图所示，点P为∠AOB的平分线上一点，PC⊥OA于C，∠OAP+∠OBP=180°，求证：OA+OB=2OC．
若有理数m，n在数轴上的位置如图所示，则（m+n）（m-n）＞0．填“＞”、“＜”或“=”）
如图，过矩形ABCD对角线AC的中点O作EF⊥AC，交BC边于点E，交AD边于点F，分别连接AE、CF．若AB=$\sqrt{3}$，∠DCF=30°，则EF长为2．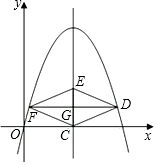
如图，在平面直角坐标系中，抛物线y=-x2+bx经过点A（4，0）．直线x=2与x轴交于点C，点E是直线x=2上的一个动点，过线段CE的中点G作DF⊥CE交抛物线于D、F两点．
11．（1）计算：（$\sqrt{3}$）2-（$\frac{1}{2}$）-1+12÷（-4）
（2）化简：（x+3）2+（x+2）（x-2）-2x2．
（3）解方程：（x-3）2+2x（x-3）=0．
（2）化简：（x+3）2+（x+2）（x-2）-2x2．
（3）解方程：（x-3）2+2x（x-3）=0．
15．
如图所示的图象中所反映的过程是：王强从家跑步去体育场，在那里锻炼了一阵后，又去早餐店吃早餐，然后散步走回家．其中x表示时间，y表示王强离家的距离．以下四个说法错误的是（ ）
如图所示的图象中所反映的过程是：王强从家跑步去体育场，在那里锻炼了一阵后，又去早餐店吃早餐，然后散步走回家．其中x表示时间，y表示王强离家的距离．以下四个说法错误的是（ ）| A． | 体育场离王强家2.5千米 | |
| B． | 王强在体育场锻炼了15分钟 | |
| C． | 体育场离早餐店4千米 | |
| D． | 王强从早餐店回家的平均速度是3千米/小时 |