题目内容
(1)通过计算,我们可以知道,方程x+
=2+
的解是x=2,x=
;方程x+
=3+
的解是x=3,x=
;方程x+
=4+
的解是x=4,x=
;…
(2)观察上述方程及方程解的特征,请你猜想关于x的方程方程x+
=c+
(c≠0)的解是 .
(3)由上述方程可知关于x的方程方程x+
=a+
(a+1≠0)的解是
(4)试用上述方法解方程:(x2+x+2)2+1=
(x2+x+2)
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| x |
| 1 |
| 4 |
| 1 |
| 4 |
(2)观察上述方程及方程解的特征,请你猜想关于x的方程方程x+
| 1 |
| x |
| 1 |
| c |
(3)由上述方程可知关于x的方程方程x+
| 1 |
| x+1 |
| 1 |
| a+1 |
(4)试用上述方法解方程:(x2+x+2)2+1=
| 5 |
| 2 |
考点:分式方程的解
专题:规律型
分析:(2)由(1)的形式即可猜想方程的解;
(3)先将原方程转化为:x+1+
=a+1+
的形式,然后得到:x+1=a+1和x+1=
,然后解得即可;
(4)先将原方程两边同时除以(x2+x+2),得到:x2+x+2+
=2+
,进而转化为:x2+x+2=2,或x2+x+2=
,然后解得即可.
(3)先将原方程转化为:x+1+
| 1 |
| x+1 |
| 1 |
| a+1 |
| 1 |
| a+1 |
(4)先将原方程两边同时除以(x2+x+2),得到:x2+x+2+
| 1 |
| x2+x+2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(2)由(1)的形式可猜想方程的解为:x=c或x=
,
经检验,x=c或x=
是原方程的解,
故答案为:x=c或x=
;
(3)原方程x+
=a+
可化为:
x+1+
=a+1+
所以x+1=a+1或x+1=
,
解得:x=a或x=-
,
经检验,x=a或x=-
是原方程的解,
故答案为:x=a或x=-
;
(4)由(x2+x+2)2+1=
(x2+x+2),可知x2+x+2≠0,
所以,原方程两边同时除以(x2+x+2),得:
x2+x+2+
=2+
,
所以x2+x+2=2①,或x2+x+2=
②,
解①得:x=0或x=-1,
经检验,x=0或x=-1是原方程的解,
故原方程的解为:x=0或x=-1.
| 1 |
| c |
经检验,x=c或x=
| 1 |
| c |
故答案为:x=c或x=
| 1 |
| c |
(3)原方程x+
| 1 |
| x+1 |
| 1 |
| a+1 |
x+1+
| 1 |
| x+1 |
| 1 |
| a+1 |
所以x+1=a+1或x+1=
| 1 |
| a+1 |
解得:x=a或x=-
| a |
| a+1 |
经检验,x=a或x=-
| a |
| a+1 |
故答案为:x=a或x=-
| a |
| a+1 |
(4)由(x2+x+2)2+1=
| 5 |
| 2 |
所以,原方程两边同时除以(x2+x+2),得:
x2+x+2+
| 1 |
| x2+x+2 |
| 1 |
| 2 |
所以x2+x+2=2①,或x2+x+2=
| 1 |
| 2 |
解①得:x=0或x=-1,
经检验,x=0或x=-1是原方程的解,
故原方程的解为:x=0或x=-1.
点评:此题考查了分式方程的解,解题的关键是:将方程转化为:x+
=c+
的形式.
| 1 |
| x |
| 1 |
| c |

练习册系列答案
相关题目
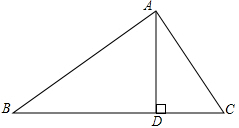 在△ABC中,AD⊥BC,tan∠B=cos∠CAD,求证:AC=BD.
在△ABC中,AD⊥BC,tan∠B=cos∠CAD,求证:AC=BD.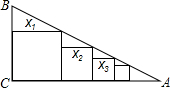 如图,在Rt△ABC中,∠C=90°,BC=a,AC=b,在△ABC中依次放入边长为x1,x2,x3,…,xn的正方形,试用a、b表示这些正方形的边长.
如图,在Rt△ABC中,∠C=90°,BC=a,AC=b,在△ABC中依次放入边长为x1,x2,x3,…,xn的正方形,试用a、b表示这些正方形的边长.