题目内容
7.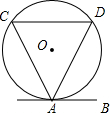 如图,直线AB与⊙O相切于点A,弦CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AD的长为( )
如图,直线AB与⊙O相切于点A,弦CD∥AB,若⊙O的半径为$\frac{5}{2}$,CD=4,则弦AD的长为( )| A. | 4 | B. | 2$\sqrt{5}$ | C. | 5 | D. | 6 |
分析 连结OA,OA的反向延长线交CD于E,连结OD,如图,根据切线的性质得AE⊥AB,再利用平行线的性质得AE⊥CD,则根据垂径定理得到CE=DE=$\frac{1}{2}$CD=2,然后根据勾股定理,在Rt△OED中计算出OE=$\frac{3}{2}$,从而得到AE的长,然后在Rt△ADE中可计算出AD.
解答 解:连结OA,OA的反向延长线交CD于E,连结OD,如图,
∵直线AB与⊙O相切于点A,
∴AE⊥AB,
∵CD∥AB,
∴AE⊥CD,
∴CE=DE=$\frac{1}{2}$CD=2,
在Rt△OED中,OE=$\sqrt{O{D}^{2}-D{E}^{2}}$=$\sqrt{(\frac{5}{2})^{2}-{2}^{2}}$=$\frac{3}{2}$,
∴AE=AO+OE=$\frac{5}{2}$+$\frac{3}{2}$=4,
在Rt△ADE中,AD=$\sqrt{D{E}^{2}+A{E}^{2}}$=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$.
故选B.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.简记作:见切点,连半径,见垂直.

练习册系列答案
相关题目
18.小明、小亮同时为校园文化艺术节制作彩旗,已知小明每小时比小亮多做5面彩旗,小明做60面彩旗与小亮做50面彩旗所用时间相同,问小明每小时做多少面彩旗?若设小明每小时做x面彩旗,则下列方程组符合题意的是( )
| A. | $\frac{60}{x}$=$\frac{50}{x-5}$ | B. | $\frac{50}{x}$=$\frac{60}{x-5}$ | C. | $\frac{60}{x}$=$\frac{50}{x+5}$ | D. | $\frac{50}{x}$=$\frac{60}{x+5}$ |
16.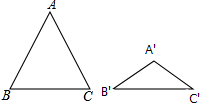 如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为( )
如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为( )
 如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为( )
如图,△ABC与△A′B′C′都是等腰三角形,且AB=AC=5,A′B′=A′C′=3,若∠B+∠B′=90°,则△ABC与△A′B′C′的面积比为( )| A. | 25:9 | B. | 5:3 | C. | $\sqrt{5}$:$\sqrt{3}$ | D. | 5$\sqrt{5}$:3$\sqrt{3}$ |
17. 如图所示几何体的俯视图是( )
如图所示几何体的俯视图是( )
 如图所示几何体的俯视图是( )
如图所示几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
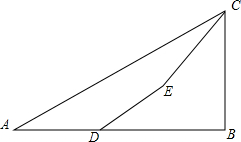 如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地而上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1:$\sqrt{3}$,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:$\sqrt{3}$是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取$\sqrt{3}$=1.732,结果精确到0.1m).
如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地而上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1:$\sqrt{3}$,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:$\sqrt{3}$是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取$\sqrt{3}$=1.732,结果精确到0.1m).