题目内容
5.计算(a${\;}^{\frac{4}{5}}$-b${\;}^{\frac{4}{5}}$)÷(a${\;}^{\frac{2}{5}}$+b${\;}^{\frac{2}{5}}$)÷(a${\;}^{\frac{1}{5}}$+b${\;}^{\frac{1}{5}}$)分析 根据平方差公式和除法法则进行化简即可解答本题.
解答 解:(a${\;}^{\frac{4}{5}}$-b${\;}^{\frac{4}{5}}$)÷(a${\;}^{\frac{2}{5}}$+b${\;}^{\frac{2}{5}}$)÷(a${\;}^{\frac{1}{5}}$+b${\;}^{\frac{1}{5}}$)
=$({a}^{\frac{2}{5}}+{b}^{\frac{2}{5}})({a}^{\frac{2}{5}}-{b}^{\frac{2}{5}})$×$\frac{1}{{a}^{\frac{2}{5}}+{b}^{-\frac{2}{5}}}×\frac{1}{{a}^{\frac{1}{5}}+{b}^{\frac{1}{5}}}$
=$({a}^{\frac{2}{5}}-{b}^{\frac{2}{5}})×\frac{1}{{a}^{\frac{1}{5}}+{b}^{\frac{1}{5}}}$
=$({a}^{\frac{1}{5}}+{b}^{\frac{1}{5}})({a}^{\frac{1}{5}}-{b}^{\frac{1}{5}})×\frac{1}{{a}^{\frac{1}{5}}+{b}^{\frac{1}{5}}}$
=${a}^{\frac{1}{5}}-{b}^{\frac{1}{5}}$.
点评 本题考查分数指数幂,解题的关键是巧妙的利用平方差公式化简.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
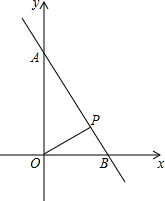 如图,在平面直角坐标系中.已知点A(0,1+$\sqrt{3}$)和B(1+$\sqrt{3}$,0),点P在线段AB上,∠BOP=30°.
如图,在平面直角坐标系中.已知点A(0,1+$\sqrt{3}$)和B(1+$\sqrt{3}$,0),点P在线段AB上,∠BOP=30°.