题目内容
7.如图(图1),点M、N分别是正方形ABCD的边AB、AD的中点,连接CN、DM.(1)求证:△ADM≌△DCN;
(2)如图(图2),设CN、DM的交点为H,连接BH,求证:BC=BH;
(3)将△ADM沿DM翻折得到△A′DM,延长MA′交DC的延长线于点E,如图(图3),求tan∠DEM.

分析 (1)根据正方形的性质、全等三角形的判定定理证明△ADM≌△DCN;
(2)延长DM、CB交于点P,根据平行线的性质得到BP=AD,根据直角三角形的性质证明即可;
(3)根据翻转变换的性质得到∠AMD=∠DME,根据平行线的性质、等腰三角形的判定定理得到EM=ED,根据勾股定理、正弦的概念计算即可.
解答 证明:(1)∵点M、N分别是正方形ABCD的边AB、AD的中点,
∴AM=DN.AD=DC.∠A=∠CDN,
在△AMD和△DNC中,
$\left\{\begin{array}{l}{AM=DN}\\{∠A=∠CDN}\\{AD=DC}\end{array}\right.$,
∴△AMD≌△DNC(SAS);
(2)如图2,延长DM、CB交于点P,
∵AD∥BC,MA=MB,
∴BP=AD=BC.
∵由(1)可得∠CHP=90°,
∴∠PHC=90°,
∴BH=$\frac{1}{2}$PC=BC;
(3)∵将△ADM沿DM翻折得到△A′DM,
∴∠AMD=∠DME,
∵AB∥DC,
∴∠EDM=∠AMD=∠DME,
∴EM=ED.
设AD=A′D=4a,则A′M=AM=2a,
∴DE=ME=EA′+2a.
在Rt△DA′E中,A′D2+A′E2=DE2,
∴(4a)2+A′E2=(EA′+2a)2,
解得A′E=3a,
∴在直角△A′DE中,tan∠DEM=A′D:A′E=$\frac{4}{3}$.
点评 本题考查的是全等三角形的判定和性质、相似三角形的判定和性质、正弦的概念、翻转变换的性质以及勾股定理的应用,掌握翻转变换是轴对称、全等三角形、相似三角形的判定定理和性质定理是解题的关键.

练习册系列答案
相关题目
17.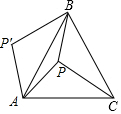 P为△ABC内一点,且PA=4,PC=5,PB=3,将△APC绕点A逆时针旋转使P与P’对应,C与B对应,则四边形AP′BP的面积为( )
P为△ABC内一点,且PA=4,PC=5,PB=3,将△APC绕点A逆时针旋转使P与P’对应,C与B对应,则四边形AP′BP的面积为( )
 P为△ABC内一点,且PA=4,PC=5,PB=3,将△APC绕点A逆时针旋转使P与P’对应,C与B对应,则四边形AP′BP的面积为( )
P为△ABC内一点,且PA=4,PC=5,PB=3,将△APC绕点A逆时针旋转使P与P’对应,C与B对应,则四边形AP′BP的面积为( )| A. | 4$\sqrt{3}$+6 | B. | 12$\sqrt{3}$+6 | C. | 60 | D. | 42 |
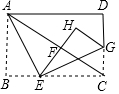 如图,将矩形纸片ABCD沿AE折叠,使点B落在对角线AC上的点F处,再沿EG折叠,使点C落在矩形内的点H处,且E、F、H在同一直线上,若AB=6,BC=8,则CG的长是$\frac{5}{2}$.
如图,将矩形纸片ABCD沿AE折叠,使点B落在对角线AC上的点F处,再沿EG折叠,使点C落在矩形内的点H处,且E、F、H在同一直线上,若AB=6,BC=8,则CG的长是$\frac{5}{2}$.
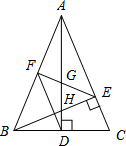 如图,在△ABC中,AB=AC,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确结论的序号是①②③④.(把你认为正确结论的序号都填上).
如图,在△ABC中,AB=AC,AD和BE是高,∠ABE=45°,点F是AB的中点,AD与FE、BE分别交于点G、H.有下列结论:①FD=FE;②AH=2CD;③BC•AD=$\sqrt{2}$AE2;④S△ABC=4S△ADF.其中正确结论的序号是①②③④.(把你认为正确结论的序号都填上).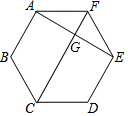 如图,在正六边形ABCDEF中,连接CF,AE,则$\frac{FG}{CG}$的值为$\frac{1}{3}$.
如图,在正六边形ABCDEF中,连接CF,AE,则$\frac{FG}{CG}$的值为$\frac{1}{3}$.