题目内容
9.如图的四个图形中,既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有( )个.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据旋转、轴对称的定义来分析.图形的旋转是图形上的每一点在平面上绕某个固定点旋转固定角度的位置移动;轴对称是指如果一个图形沿一条直线折叠,直线两侧的图形能够互相重合,就是轴对称.
解答 解:图形①可以分别旋转90°得到,也可以经过轴对称,沿一条直线对折,能够完全重合;
图形②可以旋转90°得到,也可以经过轴对称,沿一条直线对折,能够完全重合;
图形③可以旋转180°得到,不可以经过轴对称得到,故此选项错误;
图形④可以旋转180°得到,也可以经过轴对称,沿一条直线对折,能够完全重合.
故既可用旋转来分析整个图案的形成过程,又可用轴对称来分析整个图案的形成过程的图案有3个.
故选:C.
点评 此题考查了旋转和轴对称的性质.①旋转变化前后,对应线段、对应角分别相等,图形的大小、形状都不改变,两组对应点连线的交点是旋转中心;②轴对称图形的对应线段、对应角相等.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
19. 如图,菱形ABCD的边长是2,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
如图,菱形ABCD的边长是2,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
 如图,菱形ABCD的边长是2,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )
如图,菱形ABCD的边长是2,∠B=120°,P是对角线AC上一个动点,E是CD的中点,则PE+PD的最小值为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
20.某工厂共有60名员工,他们的月工资方差是s2,现在给每个员工的月工资增加300元,那么他们的新工资的方差( )
| A. | 变为s2+300 | B. | 不变 | C. | 变大了 | D. | 变小了 |
17.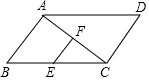 如图,在?ABCD中,E是BC边的中点,F是对角线AC的中点,若EF=5,则DC的长为( )
如图,在?ABCD中,E是BC边的中点,F是对角线AC的中点,若EF=5,则DC的长为( )
 如图,在?ABCD中,E是BC边的中点,F是对角线AC的中点,若EF=5,则DC的长为( )
如图,在?ABCD中,E是BC边的中点,F是对角线AC的中点,若EF=5,则DC的长为( )| A. | 2.5 | B. | 5 | C. | 10 | D. | 15 |
4.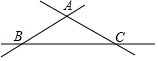 如图,直线AB、BC、AC交于A、B、C三点,则图中内错角、同位角、同旁内角的对数分别是( )
如图,直线AB、BC、AC交于A、B、C三点,则图中内错角、同位角、同旁内角的对数分别是( )
 如图,直线AB、BC、AC交于A、B、C三点,则图中内错角、同位角、同旁内角的对数分别是( )
如图,直线AB、BC、AC交于A、B、C三点,则图中内错角、同位角、同旁内角的对数分别是( )| A. | 6、12、6 | B. | 6、10、6 | C. | 4、12、4 | D. | 4、8、4 |
18. 如图,两条平行光线射向平面镜面后被反射,其中一条光线AB反射后的光线是BC,此时∠1=∠2=46°,另一条光线的反射光线EF与镜面的夹角∠3的度数为( )
如图,两条平行光线射向平面镜面后被反射,其中一条光线AB反射后的光线是BC,此时∠1=∠2=46°,另一条光线的反射光线EF与镜面的夹角∠3的度数为( )
 如图,两条平行光线射向平面镜面后被反射,其中一条光线AB反射后的光线是BC,此时∠1=∠2=46°,另一条光线的反射光线EF与镜面的夹角∠3的度数为( )
如图,两条平行光线射向平面镜面后被反射,其中一条光线AB反射后的光线是BC,此时∠1=∠2=46°,另一条光线的反射光线EF与镜面的夹角∠3的度数为( )| A. | 44° | B. | 46° | C. | 88° | D. | 54° |
19.在平面直角坐标系中,将点A(-1,3)向右平移2个单位长度,得到对应点B,则点B的坐标是( )
| A. | (-1,3) | B. | (1,3) | C. | (-3,3) | D. | (-1,5) |