题目内容
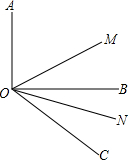 如图,OA⊥OB,OC为射线,OM平分∠AOC,ON平分∠BOC.
如图,OA⊥OB,OC为射线,OM平分∠AOC,ON平分∠BOC.(1)若∠BOC=50°,求∠MON的度数;
(2)当∠BOC的大小发生变化时,∠MON的大小发生变化吗?若不发生变化,求出∠MON的度数;若发生变化,试说明理由.
考点:角平分线的定义
专题:
分析:(1)由图示知,∠MON=∠MOC-∠NOC;然后根据角平分线的性质得到相关角的度数,代入求值即可;
(2)根据角平分线的性质和图示得到:∠MON=
(∠AOC-∠BOC)=
∠AOB.
(2)根据角平分线的性质和图示得到:∠MON=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)∵OA⊥OB,
∴∠AOB=90°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=∠AOM=
∠AOC,∠NOC=
∠BOC,
∴∠MON=∠MOC-∠NOC=
(AOC-∠BOC)=
∠AOB=45°.
(2)当∠BOC的大小发生变化时,∠MON的大小不发生变化.
由(1)知,∠MON=
∠AOB=45°.则∠MON=45°,是定值.
∴∠AOB=90°,
∵OM平分∠AOC,ON平分∠BOC,
∴∠MOC=∠AOM=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠MON=∠MOC-∠NOC=
| 1 |
| 2 |
| 1 |
| 2 |
(2)当∠BOC的大小发生变化时,∠MON的大小不发生变化.
由(1)知,∠MON=
| 1 |
| 2 |
点评:此题主要考查了垂线和角平分线的定义,要注意领会由直角得垂直这一要点.

练习册系列答案
相关题目
等腰三角形的一个内角是70°,它的一腰上的高与底边的夹角是( )
| A、35°或110° |
| B、35°或20° |
| C、20°或55° |
| D、35°或55° |

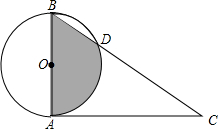 如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,∠C=30°.
如图,在⊙O中,直径AB=2,CA切⊙O于A,BC交⊙O于D,∠C=30°.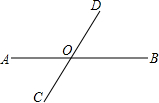 如图,直线AB,CD相交于点O,∠AOD比∠BOD大60°,求∠AOD与∠BOD的大小.
如图,直线AB,CD相交于点O,∠AOD比∠BOD大60°,求∠AOD与∠BOD的大小. 如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.连接CE,连接DE交AC于F.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.连接CE,连接DE交AC于F.