题目内容
某商场出售一种成本为20元的商品,市场调查发现,该商品每天的销售量w(千克)与销售价x(元/千克)有如下关系:w=-2x+80.设这种商品的销售利润为y(元).
(1)求y与x之间的函数关系式;
(2)在不亏本的前提下,销售价在什么范围内每天的销售利润随售价增加而增大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?
(1)求y与x之间的函数关系式;
(2)在不亏本的前提下,销售价在什么范围内每天的销售利润随售价增加而增大?最大利润是多少?
(3)如果物价部门规定这种产品的销售价不得高于28元/千克,该农户想要每天获得150元的销售利润,销售价应定为多少元?
考点:二次函数的应用,一元二次方程的应用
专题:
分析:(1)每天的销售量y×每件的利润(x-20)即为这种商品的销售利润;
(2)令销售利润为150元,得到关于x的方程,解答即可.
(2)令销售利润为150元,得到关于x的方程,解答即可.
解答:解:(1)y=w(x-20)=(-2x+80)(x-20)=-2x2+120x-1600;
(2)∵y=-2x2+120x-1600=-2(x-30)2+200,
∴售价在20-30元时,每天的销售利润随售价的增加而增加,售价为30元/千克时每天利润最大是200元.
当y=150时可得方程-2x2+120x-1600=150,
解这个方程,得 x1=25,x2=35.
根据题意,x2=35不合题意,应舍去.
∴当销售价定为25元/千克时,该农户每天可获得销售利润150元.
(2)∵y=-2x2+120x-1600=-2(x-30)2+200,
∴售价在20-30元时,每天的销售利润随售价的增加而增加,售价为30元/千克时每天利润最大是200元.
当y=150时可得方程-2x2+120x-1600=150,
解这个方程,得 x1=25,x2=35.
根据题意,x2=35不合题意,应舍去.
∴当销售价定为25元/千克时,该农户每天可获得销售利润150元.
点评:本题考查了二次函数的应用,此题为数学建模题,与利润问题相结合,借助二次函数解决实际问题.

练习册系列答案
相关题目
将一次函数图象y=2x向右平移1个单位,所得图象对应的函数关系式为( )
| A、y=2x-2 |
| B、y=2x-1 |
| C、y=2x+1 |
| D、y=2x+2 |
 如图,点C为线段AB上一点,D为AC的中点,点E为线段BD的中点.
如图,点C为线段AB上一点,D为AC的中点,点E为线段BD的中点.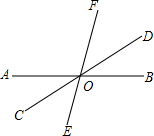 如图,已知直线AB,CD,EF相交于点O,∠COE:∠BOE=2:7,∠BOD=30°,求∠BOF的度数.
如图,已知直线AB,CD,EF相交于点O,∠COE:∠BOE=2:7,∠BOD=30°,求∠BOF的度数. 如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=1,DC=2,点P是AB上的动点,则PC+PD的最小值为
如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=1,DC=2,点P是AB上的动点,则PC+PD的最小值为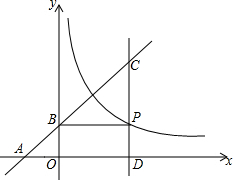 如图,直线y=x+m分别交坐标轴于A、B两点,且交平行于y轴的直线CD:x=n于点C;过点B作BP⊥CD,垂足为P.已知△OAB与△BPC的面积和为30,四边形OBPD的周长为20.若点P为反比例函数y=
如图,直线y=x+m分别交坐标轴于A、B两点,且交平行于y轴的直线CD:x=n于点C;过点B作BP⊥CD,垂足为P.已知△OAB与△BPC的面积和为30,四边形OBPD的周长为20.若点P为反比例函数y=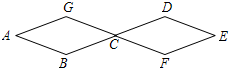 如图所示,两个全等菱形的边长为1厘米,一只蚂蚁由A点开始按ABCDEF的顺序按菱形的边循环运动,行走2015厘米后停下,则这只蚂蚁停在( )
如图所示,两个全等菱形的边长为1厘米,一只蚂蚁由A点开始按ABCDEF的顺序按菱形的边循环运动,行走2015厘米后停下,则这只蚂蚁停在( )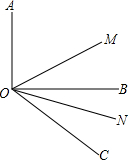 如图,OA⊥OB,OC为射线,OM平分∠AOC,ON平分∠BOC.
如图,OA⊥OB,OC为射线,OM平分∠AOC,ON平分∠BOC.