题目内容
11.用换元法解方程$\frac{y}{{y}^{2}-3}$+$\frac{{y}^{2}-3}{y}$=$\frac{5}{2}$时,如果设x=$\frac{y}{{y}^{2}-3}$,那么原方程可化为( )| A. | 2x2-5x+2=0 | B. | x2-5x+1=0 | C. | 2x2+5x+2=0 | D. | 2x2-5x+1=0 |
分析 根据换元法,可得关于x的分式方程,根据等式的性质,可得整式方程.
解答 解:换元法解方程$\frac{y}{{y}^{2}-3}$+$\frac{{y}^{2}-3}{y}$=$\frac{5}{2}$时,如果设x=$\frac{y}{{y}^{2}-3}$,那么原方程可化为2x+2×$\frac{1}{x}$-5=0,
化简,得2x2-5x+2=0,
故选:A.
点评 本题考查了换元法解分式方程,换元是解题关键,注意要化简成整式方程.

练习册系列答案
相关题目
2.我们知道,每年的4月23日是”世界读书日”,某校为了鼓励学生去发现读书的乐趣,享受阅读的过程,随机调查了部分学生,就”你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表.请根据统计表提供的信息解答下列问题:
(1)这次随机调查了200名学生,统计表中d=0.13.
(2)假如以此统计表绘制出扇形统计图,则武侠小说对应的圆心角度数是多少?
| 各类 | 频数 | 频率 |
| 卡通画 | a | 0.56 |
| 时文杂志 | 32 | b |
| 武侠小说 | 30 | 0.15 |
| 文学名著 | c | d |
(2)假如以此统计表绘制出扇形统计图,则武侠小说对应的圆心角度数是多少?
20. 如图,是由三个正方形组成的图形,则∠1+∠2+∠3等于( )
如图,是由三个正方形组成的图形,则∠1+∠2+∠3等于( )
 如图,是由三个正方形组成的图形,则∠1+∠2+∠3等于( )
如图,是由三个正方形组成的图形,则∠1+∠2+∠3等于( )| A. | 60° | B. | 90° | C. | 120° | D. | 180° |
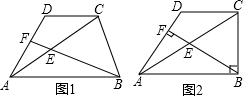 如图1,在梯形ABCD中,AB∥CD,AC=2CD,AB=nDC,E为对角线AC的中点.
如图1,在梯形ABCD中,AB∥CD,AC=2CD,AB=nDC,E为对角线AC的中点.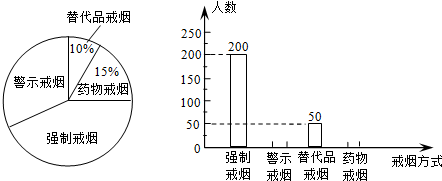
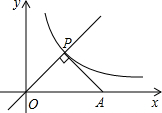 如图,点P是正比例函数y=x与反比例函数y=$\frac{k}{x}$在第一象限内的交点,PA⊥OP交x轴于点A,△POA的面积为3,则k的值是3.
如图,点P是正比例函数y=x与反比例函数y=$\frac{k}{x}$在第一象限内的交点,PA⊥OP交x轴于点A,△POA的面积为3,则k的值是3.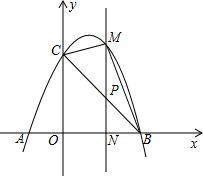 如图,已知抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC.
如图,已知抛物线y=-x2+2x+3与x轴交于A,B两点(点A在点B的左边),与y轴交于点C,连接BC. 如图,E,F是菱形ABCD对角线上的两点,且AE=CF.
如图,E,F是菱形ABCD对角线上的两点,且AE=CF.