题目内容
16.在菱形ABCD中,∠ABC=60°,BC=6$\sqrt{3}$,点E在AB上,CE=2$\sqrt{7}$,将CE绕点C旋转60°得到的线段与BD相交于点F,请你画出图形,直接写出DF的长,并画出体现解法的辅助线.分析 如图,作CH⊥AB于H,E′Q⊥BD于Q,根据菱形的性质得BA=BC,AC⊥BD,BO=$\frac{1}{2}$BD=3$\sqrt{3}$,OA=OC,则可判断△ABC为等边三角形,得到OC=$\frac{\sqrt{3}}{3}$OB=3,CH=OB=3$\sqrt{3}$,接着利用勾股定理计算出EH=1,则AE=2,然后根据旋转的性质得DE′=AE=2,在Rt△DE′Q中利用含30度的直角三角形三边的关系得∠E′Q=$\frac{1}{2}$DE′=1,DQ=$\sqrt{3}$E′Q=$\sqrt{3}$,再根据平行线分线段成比例定理可计算出QF=$\frac{\sqrt{3}}{2}$,于是得到DF=$\frac{3\sqrt{3}}{2}$.
解答 解:如图,
作CH⊥AB于H,E′Q⊥BD于Q,
∵四边形ABCD为菱形,
∴BA=BC,AC⊥BD,BO=$\frac{1}{2}$BD=3$\sqrt{3}$,OA=OC,
而∠ABC=60°,
∴△ABC为等边三角形,
∴OC=$\frac{\sqrt{3}}{3}$OB=3,CH=OB=3$\sqrt{3}$,
∴AH=BH=3,
在Rt△CHE中,EH=$\sqrt{C{E}^{2}-C{H}^{2}}$=$\sqrt{(2\sqrt{7})^{2}-(3\sqrt{3})^{2}}$=1,
∴AE=2,
∵CE绕点C旋转60°得到的线段与BD相交于点F,
而∠ACD=60°,CA=CD,
∴△CAE旋转60°得到△CDE′,
∴DE′=AE=2,
在Rt△DE′Q中,∵∠E′DQ=30°,
∴∠E′Q=$\frac{1}{2}$DE′=1,DQ=$\sqrt{3}$E′Q=$\sqrt{3}$,
∴OQ=OD-DQ=3$\sqrt{3}$-$\sqrt{3}$=2$\sqrt{3}$,
∵E′Q∥OC,
∴$\frac{QF}{OF}$=$\frac{E′Q}{OC}$=$\frac{1}{3}$,
∴QF=$\frac{1}{4}$OQ=$\frac{\sqrt{3}}{2}$,
∴DF=DQ+QF=$\sqrt{3}$+$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.也考查了旋转的性质、等边三角形的性质和含30度的直角三角形三边的关系.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案| 套餐使用费(单位:元/月) | 套餐内包含国内主叫通话时长(单位:分钟) | 套餐外国内主叫通话单价(单位:元/分钟) | 国内被叫 | 套餐内包含国内数据流量(单位:兆) | 套餐外国内数据流量单价(单位:元/兆) |
| 58 | 150 | 0.25 | 免费 | 30 | 0.50 |
| 88 | 350 | 0.19 | 免费 | 30 | 0.50 |
(2)如果某用户某月国内主叫通话总时长为250分钟,使用国内数据流量为90兆(字节),上述两种套餐中他选哪一种较为合算?
| A. | 1 | B. | -1 | C. | 3 | D. | -3 |
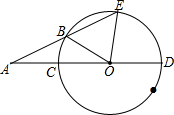 如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,则∠A的度数是28°.
如图,CD是⊙O的直径,∠EOD=84°,AE交⊙O于点B,且AB=OC,则∠A的度数是28°.