题目内容
9.抛物线经过A(-1,0),B(3,0),过(0,-2)点的直线l与x轴平行,抛物线与直线l有交点,结合函数图象,求a的取值范围.分析 求得对称轴,如果过(0,-2)点的直线l与x轴平行,抛物线与直线l有交点,则开口向上,当顶点为(1,-2)时求得a的值,即可求得a的取值.
解答 解:∵物线经过A(-1,0),B(3,0),
∴对称轴x=$\frac{-1+3}{2}$=1,
当抛物线的顶点为(1,-2)时,则y=a(x-1)2-2,
代入(-1,0)得,4a-2=0,
解得a=$\frac{1}{2}$,
所以过(0,-2)点的直线l与x轴平行,抛物线与直线l有交点,则a的取值范围为a≥$\frac{1}{2}$.
点评 本题考查了二次函数图象上点的坐标特征,求得顶点为(1,-2)时的a的值是解题的关键.

练习册系列答案
相关题目
4.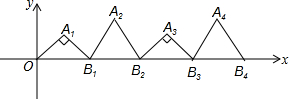 如图,在平面直角坐标系的第一象限内,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐标为(2,0),B2坐标为(4,0),B3坐标为(6,0),…,按这样的规律,点A2015的坐标是( )
如图,在平面直角坐标系的第一象限内,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐标为(2,0),B2坐标为(4,0),B3坐标为(6,0),…,按这样的规律,点A2015的坐标是( )
 如图,在平面直角坐标系的第一象限内,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐标为(2,0),B2坐标为(4,0),B3坐标为(6,0),…,按这样的规律,点A2015的坐标是( )
如图,在平面直角坐标系的第一象限内,依次作等腰直角三角形OA1B1,正三角形B1A2B2,等腰直角三角形B2A3B3,…,且∠A1=∠A3=∠A5=…=90°,B1坐标为(2,0),B2坐标为(4,0),B3坐标为(6,0),…,按这样的规律,点A2015的坐标是( )| A. | (4029,1) | B. | (2015,$\sqrt{3}$) | C. | (4030,1) | D. | (4029,$\sqrt{3}$) |
18.若$\frac{4a}{4-|a|}$有意义,则$\frac{4a}{4-a}$的值( )
| A. | 无意义 | B. | 有意义 | C. | 值为0 | D. | 以上答案都不对 |
19.如果在Rt△ABC中,∠C=90°,AC=2,BC=3,那么下列各式正确的是( )
| A. | tanB=$\frac{2}{3}$ | B. | cotB=$\frac{2}{3}$ | C. | sinB=$\frac{2}{3}$ | D. | cosB=$\frac{2}{3}$ |
 如图,一个长方形运动场被分隔成A、B、A、B、C共5个区,A区是边长为am的正方形,C区是边长为bm的正方形.
如图,一个长方形运动场被分隔成A、B、A、B、C共5个区,A区是边长为am的正方形,C区是边长为bm的正方形.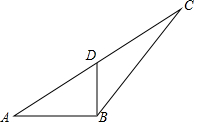 如图,已知△ABC中,中线BD⊥AB,AB=6,BD=4,求tan∠CBD的值.
如图,已知△ABC中,中线BD⊥AB,AB=6,BD=4,求tan∠CBD的值.