题目内容
18.已知抛物线y=-$\frac{1}{2}$(x-1)(2-x),它的图象在对称轴左侧的部分是下降(填“上升”、“下降”).分析 根据y=ax2+bx+c(a,b,c为常数,a≠0),当a>0时,在对称轴左侧y随x的增大而减小,可得答案.
解答 解:抛物线y=-$\frac{1}{2}$(x-1)(2-x)=$\frac{1}{2}$x2-$\frac{3}{2}$x+1,
a=$\frac{1}{2}$>0,它的图象在对称轴左侧的部分是下降,
故答案为:下降.
点评 本题考查了二次函数的性质,二次函数y=ax2+bx+c(a,b,c为常数,a≠0),当a>0时,在对称轴左侧y随x的增大而减小,在对称轴右侧y随x的增大而增大;当a<0时,在对称轴左侧y随x的增大而增大,在对称轴右侧y随x的增大而减小.正比例函数中当k>0时,y随x的增大而增大,k<0时,y随x的怎大而减小.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
9.三角形两边的垂直平分线的交点为O,则点O( )
| A. | 到三边距离相等 | B. | 到三顶点距离相等 | ||
| C. | 不在第三边的垂直平分线上 | D. | 以上都不对 |
6.下列各式中,代数式的个数是( )
①$\frac{1}{2}$ ②26+a ③b=ba ④$\frac{1}{x+y}$ ⑤2a-1 ⑥a ⑦$\frac{1}{2}$(a2-b2) ⑧5n+2.
①$\frac{1}{2}$ ②26+a ③b=ba ④$\frac{1}{x+y}$ ⑤2a-1 ⑥a ⑦$\frac{1}{2}$(a2-b2) ⑧5n+2.
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
3.“从一布袋中随机地摸出一枚围棋棋子,恰是黑色的概率为$\frac{2}{5}$”的意思是( )
| A. | 摸5次一定能摸到2枚黑子 | |
| B. | 摸5次一定有3次摸到白子 | |
| C. | 摸若干次,平均每5次有2次摸到黑子 | |
| D. | 袋中一定有2枚黑子,3枚白子 |
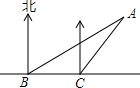 如图,海中有一小岛.它周围20海里内有暗礁.一货船由西向东航行.在B点测得岛A在北偏东65°的方向上,航行30海里到达C点.这时小岛A在北偏东40°处.如果货船不改变方向.继续向东航行,有没有触礁的危险?并说明理由.(参考数据:sin50°=0.77,cos50°=0.64,tan50°=1.19).
如图,海中有一小岛.它周围20海里内有暗礁.一货船由西向东航行.在B点测得岛A在北偏东65°的方向上,航行30海里到达C点.这时小岛A在北偏东40°处.如果货船不改变方向.继续向东航行,有没有触礁的危险?并说明理由.(参考数据:sin50°=0.77,cos50°=0.64,tan50°=1.19). 如图,在⊙O中,CD为直径,AB为弦,且CD平分AB于E,OE=3cm,AB=8cm,则⊙O的半径为5.
如图,在⊙O中,CD为直径,AB为弦,且CD平分AB于E,OE=3cm,AB=8cm,则⊙O的半径为5.