题目内容
 如图,D是△ABC内的一点,连接BD并延长到点E,连接AD、AE,若
如图,D是△ABC内的一点,连接BD并延长到点E,连接AD、AE,若| AD |
| AB |
| DE |
| BC |
| AE |
| AC |
考点:相似三角形的判定与性质
专题:
分析:由条件可证得△ADE∽△ABC,可得∠DAE=∠BAC,即∠BAD+∠DAC=∠DAC+∠CAE,可得∠BAD=∠CAE,可得出答案.
解答:解:
∵
=
=
,
∴△ADE∽△ABC,
∴∠DAE=∠BAC,
∴∠BAD+∠DAC=∠DAC+∠CAE,
∴∠BAD=∠CAE=29°,
故答案为:29°.
∵
| AD |
| AB |
| DE |
| BC |
| AE |
| AC |
∴△ADE∽△ABC,
∴∠DAE=∠BAC,
∴∠BAD+∠DAC=∠DAC+∠CAE,
∴∠BAD=∠CAE=29°,
故答案为:29°.
点评:本题主要考查相似三角形的判定和性质,掌握相似三角形的对应角相等是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 如图,⊙O中,若∠AOC=150°,那么∠ABC=( )
如图,⊙O中,若∠AOC=150°,那么∠ABC=( )| A、150° | B、125° |
| C、105° | D、100° |
找出“3,7,15,( ),63”的规律,括号理应填( )
| A、46 | B、27 | C、30 | D、31 |
 二次函数y=ax2+bx+c(a≠0)的图象如图,下列4个结论中结论正确的有
二次函数y=ax2+bx+c(a≠0)的图象如图,下列4个结论中结论正确的有 直线AD上有A、B、C、D四个站,要建1个加油站M,使得加油站M到各个站之间路程和最小,问加油站建在何处.
直线AD上有A、B、C、D四个站,要建1个加油站M,使得加油站M到各个站之间路程和最小,问加油站建在何处. 如图,已知
如图,已知 已知,∠BAC=∠BDC=90°,点E在BC上,且BE=EC,P点为AD外一点,且PA=PD,求证:PE垂直平分AD.
已知,∠BAC=∠BDC=90°,点E在BC上,且BE=EC,P点为AD外一点,且PA=PD,求证:PE垂直平分AD.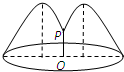 如图,花坛水池中央有一喷泉,水管OP=3m,水从喷头P喷出后呈抛物线状先向上至最高点后落下,若最高点距水面4m,P距抛物线对称轴1m,则为使水不落到池外,水池半径最小为( )
如图,花坛水池中央有一喷泉,水管OP=3m,水从喷头P喷出后呈抛物线状先向上至最高点后落下,若最高点距水面4m,P距抛物线对称轴1m,则为使水不落到池外,水池半径最小为( )