题目内容
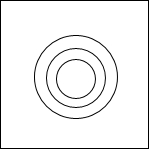某健身俱乐部设置了如图所示的一个投镖靶，该靶是边长为18cm的正方形木板，镖靶从中心往外依次画有半径分别为1cm、2cm和3cm的同心圆，当投镖者投中最里层最小的圆时，获得一等奖；当投中小圆与中间圆围成的圆环时，可获得二等奖；当投中中圆与最大的圆围成的圆环时，可获得三等奖．若每人只投一镖，请你分别求出获得第一名和第三名的概率．（结果精确到0.01）考点：几何概率
专题：
分析：最里层最小的圆的面积除以正方形木板的面积为获得第一名的概率；中圆与最大的圆围成的圆环的面积除以正方形木板的面积为获得第三名的概率．
解答：解：∵
≈0.01，
∴获得第一名的概率约为0.01；
∵
≈0.05，
∴获得第三名的概率约为0.05．
| π×12 |
| 18×18 |
∴获得第一名的概率约为0.01；
∵
| π(32-22) |
| 18×18 |
∴获得第三名的概率约为0.05．
点评：本题将概率的求解设置于飞镖随意投中如图所示的正方形木板的游戏中，考查学生对简单几何概型的掌握情况，既避免了单纯依靠公式机械计算的做法，又体现了数学知识在现实生活、甚至娱乐中的运用，体现了数学学科的基础性．用到的知识点为：概率=相应的面积与总面积之比．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
矩形ABCD沿对角线BD翻折BCD为BC′D，设C′B与AD交点为E，△BED面积为整个矩形面积的
如图所示，分别求出扇形丙、丁的圆心角及甲、乙的面积比．在坐标系中，P点的坐标是（cos30°，tan45°），则P点关于x轴对称点Q的坐标为（ ）
A、（
| ||||
B、（-1，
| ||||
C、（
| ||||
D、（-
|