Question

7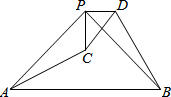．如图，△PAB与△PCD都是等腰直角三角形，∠APB=∠CPD=90°，连结AC、BD，求证：△PAC≌△PBD．

Answer 1

分析 求出PA=PB，PC=PD，∠APC=∠BPD，根据全等三角形的判定定理推出即可．

解答 证明：∵△PAB与△PCD都是等腰直角三角形，
∴PA=PB，PC=PD．
∵∠APB=∠CPD=90°，
∴∠APB-∠BPC=∠CPD-∠BPC，
即∠APC=∠BPD．
在△PAC和△PBD中
$\left\{\begin{array}{l}{PA=PB}\\{∠APC=∠BPD}\\{PC=PD}\end{array}\right.$，
∴△PAC≌△PBD．

点评 本题考查了等腰直角三角形的性质，全等三角形的判定的应用，能正确运用全等三角形的判定定理进行推理是解此题的关键，难度适中．