题目内容
2.如图,将一张三角形纸片ABC折叠,使点A落在BC边上,折痕EF∥BC,得到△EFG;再继续将纸片沿△BFG的对称轴EM折叠,依照上述做法,再将△CFG折叠,最终得到矩形EMNF,折叠后的△EMG和△FNG的面积分别为1和2,则△ABC的面积为12.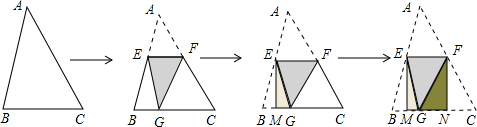
分析 根据翻折不变性,即可得到多组三角形全等:△EBM≌△EGM,△FCN≌△FGN,△AEF≌△GEF;根据同底等高的三角形全等,得到S△EMG+S△FNG=S△EFG,然后解答即可.
解答 解:根据翻折不变性,可得△EBM≌△EGM,△FCN≌△FGN,△AEF≌△GEF,
易得S△EMG+S△FNG=S△EFG,
则S△ABC=4S△EGF=4×(1+2)=12.
点评 本题考查了翻折变换,抓住翻折前后两图形全等是解题的关键.

练习册系列答案
相关题目
14.一组数据:10、5、15、5、20,则这组数据的平均数和中位数分别是( )
| A. | 10,10 | B. | 11,10 | C. | 11,12.5 | D. | 10,12.5 |
12.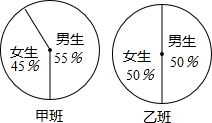 已知甲、乙组两班的总人数分别为60人和50人,两班男、女生人数的扇形统计图如图,则这两个班的女生人数为( )
已知甲、乙组两班的总人数分别为60人和50人,两班男、女生人数的扇形统计图如图,则这两个班的女生人数为( )
 已知甲、乙组两班的总人数分别为60人和50人,两班男、女生人数的扇形统计图如图,则这两个班的女生人数为( )
已知甲、乙组两班的总人数分别为60人和50人,两班男、女生人数的扇形统计图如图,则这两个班的女生人数为( )| A. | 58 | B. | 25 | C. | 27 | D. | 52 |
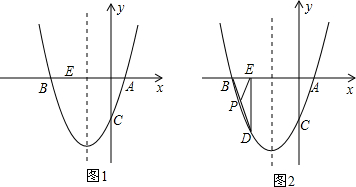
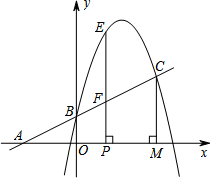 如图,已知直线y1=$\frac{1}{2}$x+b和抛物线y2=-$\frac{5}{4}$x2+ax+b都经过点B(0,1)和点C,过点C作CM⊥x轴于点M,且CM=$\frac{5}{2}$.
如图,已知直线y1=$\frac{1}{2}$x+b和抛物线y2=-$\frac{5}{4}$x2+ax+b都经过点B(0,1)和点C,过点C作CM⊥x轴于点M,且CM=$\frac{5}{2}$.