题目内容
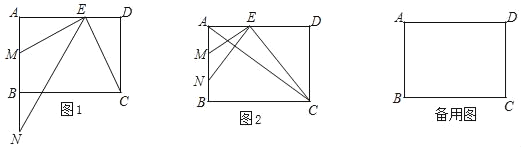
【题目】如图,△ABC是等边三角形,平面上的动点P满足PC⊥AB,记∠APB=α.
(1)如图1,当点P在直线BC上方时,直接写出∠PAC的大小(用含α的代数式表示);
(2)过点B作BC的垂线BD,同时作∠PAD=60°,射线AD与直线BD交于点D.
①如图2,判断△ADP的形状,并给出证明;
②连结CD,若在点P的运动过程中,CD=![]() AB.直接写出此时α的值.
AB.直接写出此时α的值.
【答案】(1)150°﹣![]() ;(2)①△ADP是等边三角形,证明见解析;②α=150°或α=30°.
;(2)①△ADP是等边三角形,证明见解析;②α=150°或α=30°.
【解析】
(1)由等边三角形的性质可得∠CAB=∠CBA=60°,AC=CB=AB,可证PA=PB,由等腰三角形的性质可得∠PAB=∠PBA=90°![]() ,即可求解;
,即可求解;
(2)①由“SAS”可证△DAB≌△PAC,可得AD=AP,由等边三角形的判定△ADP是等边三角形;
②分点P在直线AB上方和直线AB下方两种情况讨论,由全等三角形的性质和等腰三角形的性质可求解.
解:(1)∵△ABC是等边三角形,
∴∠CAB=∠CBA=60°,AC=CB=AB,且PC⊥AB,
∴PC垂直平分AB,
∴PA=PB,且∠APB=α,PC⊥AB,
∴∠APC=∠BPC=![]() α,
α,
∴∠PAB=∠PBA=90°﹣![]() ,
,
∴∠PAC=∠PAB+∠BAC=150°﹣![]() ;
;
(2)①△ADP是等边三角形,
理由如下:∵∠PAD=60°=∠CAB,
∴∠DAB=∠PAC,
∵△ABC是等边三角形,CP⊥AB,
∴∠ACP=∠BCP=30°,
∵DB⊥BC,∠ABC=60°
∴∠DBA=30°=∠ACP,且AC=AB,∠DAB=∠PAC,
∴△DAB≌△PAC(ASA)
∴AD=AP,且∠DAP=60°,
∴△ADP是等边三角形;
②如图3,点P在AB上方时,

∵CD=![]() AB.
AB.
∴CD=![]() BC,
BC,
∵∠DBC=90°,
∴CD2=DB2+BC2,
∴BC=DB,
∴AB=DB,且∠DBA=30°,
∴∠ADB=75°,
∵△DAB≌△PAC,
∴∠APC=∠ADB=75°,
∴α=150°;
如图4,点P在AB下方时,

∵DB⊥BC,∠ABC=60°
∴∠ABD=150°
∵CD=![]() AB.
AB.
∴CD=![]() BC,
BC,
∵∠DBC=90°,
∴CD2=DB2+BC2,
∴BC=DB,
∴AB=DB,且∠ABD=150°,
∴∠ADB=15°,
∵∠PAD=60°=∠CAB,
∴∠DAB=∠PAC,
∵△ABC是等边三角形,CP⊥AB,
∴∠ACP=∠BCP=180°﹣30°=150°,
∴∠DBA=150°=∠ACP,且AC=AB,∠DAB=∠PAC,
∴△DAB≌△PAC(SAS)
∴∠APC=∠ADB=15°,
∴α=30°,

 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案【题目】在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研其性质——运用函数解决问题”的学习过程.如图,在平面直角坐标系中己经绘制了一条直线![]() .另一函数
.另一函数![]() 与
与![]() 的函数关系如下表:
的函数关系如下表:
| … | -6 | -5 | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| … | -2 | -0.25 | 1 | 1.75 | 2 | 1.75 | 1 | -0.25 | -2 | -4.25 | -7 | -10.25 | -14 | … |
(1)求直线![]() 的解析式;
的解析式;
(2)请根据列表中的数据,绘制出函数![]() 的近似图像;
的近似图像;
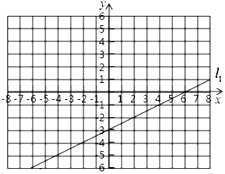
(3)请根据所学知识并结合上述信息拟合出函数![]() 的解折式,并求出
的解折式,并求出![]() 与
与![]() 的交点坐标.
的交点坐标.