题目内容
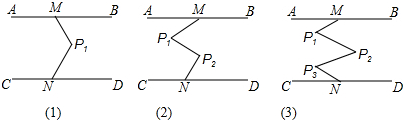
15. 如图,?ABCD中,E是BC边上一点,AD=DE,F在AE上,连CF、DF,且∠BAE=∠EDF,求证:CF=DF.
如图,?ABCD中,E是BC边上一点,AD=DE,F在AE上,连CF、DF,且∠BAE=∠EDF,求证:CF=DF.
分析 由AD=DE,∠BAE=∠EDF,可证得∠DAB=∠3+∠1=∠2+∠4=∠DFA,继而证得D,C,E,F四点共圆,然后由圆周角定理,证得∠2=∠5=∠1,得到∠3=∠6,又由圆的内接四边形的性质,证得∠3=∠CDF,继而证得结论.
解答  解:∵AD=DE,
解:∵AD=DE,
∴∠3=∠4,
∵∠BAE=∠EDF,
即∠1=∠2,
∴∠DAB=∠3+∠1=∠2+∠4=∠DFA,
∵四边形ABCD是平行四边形,
∴∠DAB=∠DCB,
∴∠DFA=∠DCB,
∴D,C,E,F四点共圆,
∴∠2=∠5=∠1,
∴∠3=∠6,
∵∠CDF+∠CEF=180°,∠3+∠CEF=180°,
∴∠3=∠CDF,
∴∠6=∠CDF,
∴DF=CF.
点评 此题考查了平行四边形的性质、等腰三角形的性质与判定以及圆周角定理.证得D,C,E,F四点共圆是解此题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
6.在△ABC中,∠A=120°,∠B=45°,∠C=15°,则cosB等于( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
7.下列命题的逆命题为真命题的是( )
| A. | 对顶角相等 | |
| B. | 两直线平行,内错角相等 | |
| C. | 全等三角形的对应角相等 | |
| D. | 如果两个实数相等,那么他们的绝对值相等 |
5.甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达A,乙客轮用20min到达B.若A、B两处的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是( )
| A. | 北偏西30° | B. | 南偏西30° | C. | 南偏东60° | D. | 南偏西30° |
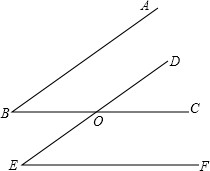 如图,已知:BC交DE于O,给出下面三个论断:①∠B=∠E;②AB∥DE;③BC∥EF.请以其中的两个论断为条件,填入“题设”栏中,以一个论断为结论,填入“结论”栏中,使之成为一个正确的命题,并加以证明.
如图,已知:BC交DE于O,给出下面三个论断:①∠B=∠E;②AB∥DE;③BC∥EF.请以其中的两个论断为条件,填入“题设”栏中,以一个论断为结论,填入“结论”栏中,使之成为一个正确的命题,并加以证明.