题目内容
10. 某水果大卖场每日批量进货销售某种水果,假设日销售量与日进货量相等.设该水果进货量为x千克,每千克进货成本为y元,每千克售价为s元,y与x的关系如图,s与x满足关系式:s=-$\frac{1}{15}$x+12.
某水果大卖场每日批量进货销售某种水果,假设日销售量与日进货量相等.设该水果进货量为x千克,每千克进货成本为y元,每千克售价为s元,y与x的关系如图,s与x满足关系式:s=-$\frac{1}{15}$x+12.(1)请解释图中线段BC的实际意义;
(2)该水果进货量为多少时,获得的日销售利润最大?最大利润是多少?
分析 (1)图中线段BC表示当进货量80≤x≤120时,每千克的进货成本均为4元;
(2)根据“获得的日销售利润=每千克的利润×进货量”分0<x<80和80≤x≤120列出函数关系式,求最大值,比较后可得.
解答 解:(1)图中线段BC表示当进货量80≤x≤120时,每千克的进货成本y=4元;
(2)设AB所在直线解析式为:y=kx+b,
由题意得:$\left\{\begin{array}{l}{b=6}\\{80k+b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{40}}\\{b=6}\end{array}\right.$,
故当0<x<80时,y=-$\frac{1}{40}$x+6,
设获得的日销售利润为W,根据题意,
①当0<x<80时,
W=[(-$\frac{1}{15}$x+12)-(-$\frac{1}{40}$x+6)]•x
=-$\frac{1}{24}$x2+6x
=-$\frac{1}{24}$(x-72)2+216,
当x=72时,W最大值=216;
②当80≤x≤120时,
W═(-$\frac{1}{15}$x+12-4)x
=-$\frac{1}{15}$x2+8x
=-$\frac{1}{15}$(x-60)2+240,
当x>60时,W随x的增大而减小,
故当x=80时,W最大值=$\frac{640}{3}$,
∵216>$\frac{640}{3}$,
∴当水果进货量为72千克时,获得的日销售利润最大,最大利润是216元.
点评 本题主要考查二次函数的实际应用能力,根据题意找到相等关系是前提和基础,分情况讨论并比较是关键.

练习册系列答案
相关题目
15.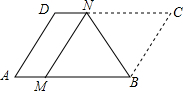 如图,将平行四边形纸片ABCD折叠,使顶点C恰好落在AB边上的点M处,折痕为BN,则关于结论:①MN∥AD;②MNCB是菱形.说法正确的是( )
如图,将平行四边形纸片ABCD折叠,使顶点C恰好落在AB边上的点M处,折痕为BN,则关于结论:①MN∥AD;②MNCB是菱形.说法正确的是( )
 如图,将平行四边形纸片ABCD折叠,使顶点C恰好落在AB边上的点M处,折痕为BN,则关于结论:①MN∥AD;②MNCB是菱形.说法正确的是( )
如图,将平行四边形纸片ABCD折叠,使顶点C恰好落在AB边上的点M处,折痕为BN,则关于结论:①MN∥AD;②MNCB是菱形.说法正确的是( )| A. | ①②都错 | B. | ①对②错 | C. | ①错②对 | D. | ①②都对 |
20.-3,-0.01,-2.7,-$\frac{1}{10}$最大的数是( )
| A. | .-3 | B. | -0.01 | C. | -2.7 | D. | -$\frac{1}{10}$ |
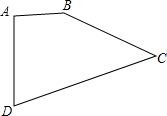 如图,已知四边形ABCD中,AB=2cm,BC=4cm,CD=5cm,AD=$\sqrt{5}$cm,∠A=90°,求四边形ABCD的面积.
如图,已知四边形ABCD中,AB=2cm,BC=4cm,CD=5cm,AD=$\sqrt{5}$cm,∠A=90°,求四边形ABCD的面积. 将“创建文明城市”六个字分别写在一个正方体的六个面上,这个正方体的平面展开图如图所示,那么在这个正方体中,和“创”相对的字是明.
将“创建文明城市”六个字分别写在一个正方体的六个面上,这个正方体的平面展开图如图所示,那么在这个正方体中,和“创”相对的字是明.
 如图,矩形ABCD中,AC、BD交于点O,AE⊥BD于E,DE=EO,0F⊥AB于F,0F=3cm,则BD=12cm.
如图,矩形ABCD中,AC、BD交于点O,AE⊥BD于E,DE=EO,0F⊥AB于F,0F=3cm,则BD=12cm.