题目内容
8.已知点P(2a-5,a+2)在第二象限,则符合条件的a的所有整数的和的立方根是( )| A. | 1 | B. | -1 | C. | 0 | D. | $\root{3}{2}$ |
分析 先判断出点P在第二象限,再根据第二象限内点的横坐标是负数,纵坐标是正数列出不等式组,然后求解即可.
解答 解:∵点P(2a-5,a+2)在第二象限,
∴$\left\{\begin{array}{l}{2a-5<0}\\{a+2>0}\end{array}\right.$
解得:$-2<a<\frac{5}{2}$
符合条件的a的所有整数为-1,0,1,2,
∴-1+0+1+2=2,
∴2的立方根为:$\root{3}{2}$,
故选:D.
点评 本题考查了各象限内点的坐标的符号特征以及解不等式,记住各象限内点的坐标的符号是解决的关键,四个象限的符号特点分别是:第一象限(+,+);第二象限(-,+);第三象限(-,-);第四象限(+,-).

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
3.若a>b,则下列式子正确的是( )
| A. | -5a>-5b | B. | a-3>b-3 | C. | 4-a>4-b | D. | $\frac{1}{2}$a<$\frac{1}{2}$b |
 如图,在四边形ABCD中,AD∥BC,∠BAD=∠BCD.
如图,在四边形ABCD中,AD∥BC,∠BAD=∠BCD.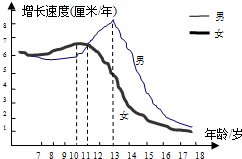 生物学研究表明,在8--17岁期间,男女生身高增长速度规律呈现如下图所示,请你观察此图,回答下列问题,男生身高增长速度的巅峰是几岁?在几岁时男生、女生的身高增长速度是一样的?
生物学研究表明,在8--17岁期间,男女生身高增长速度规律呈现如下图所示,请你观察此图,回答下列问题,男生身高增长速度的巅峰是几岁?在几岁时男生、女生的身高增长速度是一样的?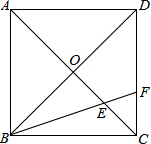 如图,在正方形ABCD中,AC、BD相交于点O,∠DBC的平分线BF交AC于点E,交DC于点F,求证:OE=$\frac{1}{2}$DF.
如图,在正方形ABCD中,AC、BD相交于点O,∠DBC的平分线BF交AC于点E,交DC于点F,求证:OE=$\frac{1}{2}$DF.