题目内容
19.一条直线经过A(-1,2),且平行于直线y=-3x+1.(1)求这条直线的解析式;
(2)求这条直线与坐标轴围成的图形的面积.
分析 (1)根据两直线平行的问题得到k=-3,然后把(-1,2)代入y=-3x+b得求出b即可得到该函数解析式为y=-3x-1;
(2)先求出直线y=-3x-1与x轴和y轴的交点坐标,然后根据三角形面积公式求解.
解答  解:(1)∵直线y=kx+b与直线y=-3x+1平行,
解:(1)∵直线y=kx+b与直线y=-3x+1平行,
∴k=-3,
把(-1,2)代入y=-3x+b得b=-1,
∴该函数解析式为y=-3x-1;
(2)当y=0时,-3x-1=0,解得x=-$\frac{1}{3}$,则直线y=-3x-1与x轴的交点的坐标为(-$\frac{1}{3}$,0),
当x=0时,-1=y,解得y=-1,则直线y=-3x-1与y轴的交点的坐标为(0,-1),
所以这条直线与坐标轴围成的图形的面积=$\frac{1}{2}×\frac{1}{3}×1=\frac{1}{6}$.
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.也考查了待定系数法求一次函数解析式.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
10. 如图,是由四个相同的正方体组合而成的两个几何体,则下列表述正确的是( )
如图,是由四个相同的正方体组合而成的两个几何体,则下列表述正确的是( )
 如图,是由四个相同的正方体组合而成的两个几何体,则下列表述正确的是( )
如图,是由四个相同的正方体组合而成的两个几何体,则下列表述正确的是( )| A. | 图甲的主视图与图乙的左视图形状相同 | |
| B. | 图甲的左视图与图乙的俯视图形状相同 | |
| C. | 图甲的俯视图与图乙的俯视图形状相同 | |
| D. | 图甲的主视图与图乙的主视图形状相同 |
7. 某班50人参加猜谜语比赛,老师把本班猜谜语活动的情况绘制如图的条形统计图,根据此图,本班猜对谜语个数的中位数和众数分别是( )
某班50人参加猜谜语比赛,老师把本班猜谜语活动的情况绘制如图的条形统计图,根据此图,本班猜对谜语个数的中位数和众数分别是( )
 某班50人参加猜谜语比赛,老师把本班猜谜语活动的情况绘制如图的条形统计图,根据此图,本班猜对谜语个数的中位数和众数分别是( )
某班50人参加猜谜语比赛,老师把本班猜谜语活动的情况绘制如图的条形统计图,根据此图,本班猜对谜语个数的中位数和众数分别是( )| A. | 18,20 | B. | 20,20 | C. | 8,8 | D. | 9,8 |
8.已知点P(2a-5,a+2)在第二象限,则符合条件的a的所有整数的和的立方根是( )
| A. | 1 | B. | -1 | C. | 0 | D. | $\root{3}{2}$ |
 如图,已知AC垂直平分BD,∠ABC=∠DAF,DF⊥BD
如图,已知AC垂直平分BD,∠ABC=∠DAF,DF⊥BD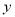 度,底角为
度,底角为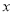 度,请写出顶角
度,请写出顶角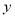 (度)与底角
(度)与底角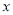 (度)之间的函数关系式__________________ ,自变量
(度)之间的函数关系式__________________ ,自变量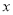 的取值范围是_____________;
的取值范围是_____________;