题目内容
17.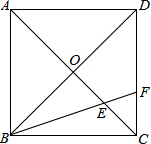 如图,在正方形ABCD中,AC、BD相交于点O,∠DBC的平分线BF交AC于点E,交DC于点F,求证:OE=$\frac{1}{2}$DF.
如图,在正方形ABCD中,AC、BD相交于点O,∠DBC的平分线BF交AC于点E,交DC于点F,求证:OE=$\frac{1}{2}$DF.
分析 作OG∥AB交BE于点G,则OG是△BDF的中位线,根据正方边形的性质求得∠AEB和∠ABE的度数,即可证明OG=OE,据此即可证得结论.
解答 证明:如图,作OG∥AB交BE于点G.
∵O是BD的中点,
∴OG是△BDF的中位线,
∴OG=$\frac{1}{2}$DF,
∵正方形ABCD中,∠ABD=∠DBC=45°,
又∵BF是∠DBC的平分线,
∴∠ABF=45°+$\frac{1}{2}$×45°=67.5°.
∵AB∥OG,
∴∠OGE=∠ABE=67.5°,
又∵在△ABE中,∠BAE=45°,
∴∠AEB=180°-45°-67.5°=67.5°,
∴∠OGE=∠AEB,
∴OE=OG,
∴OE=$\frac{1}{2}$DF.
点评 本题考查了正方形的性质、三角形的中位线定理以及等腰三角形的判定定理的综合应用,正确作出辅助线是关键.

练习册系列答案
相关题目
7. 某班50人参加猜谜语比赛,老师把本班猜谜语活动的情况绘制如图的条形统计图,根据此图,本班猜对谜语个数的中位数和众数分别是( )
某班50人参加猜谜语比赛,老师把本班猜谜语活动的情况绘制如图的条形统计图,根据此图,本班猜对谜语个数的中位数和众数分别是( )
 某班50人参加猜谜语比赛,老师把本班猜谜语活动的情况绘制如图的条形统计图,根据此图,本班猜对谜语个数的中位数和众数分别是( )
某班50人参加猜谜语比赛,老师把本班猜谜语活动的情况绘制如图的条形统计图,根据此图,本班猜对谜语个数的中位数和众数分别是( )| A. | 18,20 | B. | 20,20 | C. | 8,8 | D. | 9,8 |
8.已知点P(2a-5,a+2)在第二象限,则符合条件的a的所有整数的和的立方根是( )
| A. | 1 | B. | -1 | C. | 0 | D. | $\root{3}{2}$ |
 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D以每秒1个单位长度的速度由点A向点B匀速运动,到达B点即停止运动,M,N分别是AD,CD的中点,连接MN,设点D运动的时间为t.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D以每秒1个单位长度的速度由点A向点B匀速运动,到达B点即停止运动,M,N分别是AD,CD的中点,连接MN,设点D运动的时间为t.
 度,底角为
度,底角为 度,请写出顶角
度,请写出顶角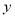 (度)与底角
(度)与底角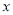 (度)之间的函数关系式__________________ ,自变量
(度)之间的函数关系式__________________ ,自变量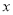 的取值范围是_____________;
的取值范围是_____________; ,求: ①
,求: ① ;
; ?
?
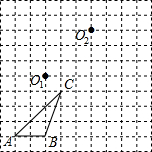 如图,网格中每个小正方形的边长均为1个单位长度
如图,网格中每个小正方形的边长均为1个单位长度