题目内容
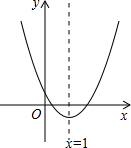 如图,二次函数y=ax2+bx+c图象的对称轴为x=1,则下列说法正确的有( )
如图,二次函数y=ax2+bx+c图象的对称轴为x=1,则下列说法正确的有( )①abc<0,②2a+b=0,③a-b+c>0,④若4a+2b+c>0.
| A、①②③ | B、②③④ |
| C、①②④ | D、①②③④ |
考点:二次函数图象与系数的关系
专题:
分析:由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答:解:A、根据图示知,抛物线开口方向向上,则a>0.
抛物线的对称轴x=-
=1>0,则b<0.
抛物线与y轴交与正半轴,则c>0,
所以abc<0.
故本选项正确;
B、∵x=-
=1,
∴b=-2a,
∴2a+b=0.
故本选项正确;
C、∵抛物线开口方向向上,与y轴交与正半轴,
∴当x=-1时,y>0,即a-b+c>0.
故本选项正确;
D、由x=2时,y=4a+2b+c,由图象知:y=4a+2b+c>0,故本选项正确;
故选D.
抛物线的对称轴x=-
| b |
| 2a |
抛物线与y轴交与正半轴,则c>0,
所以abc<0.
故本选项正确;
B、∵x=-
| b |
| 2a |
∴b=-2a,
∴2a+b=0.
故本选项正确;
C、∵抛物线开口方向向上,与y轴交与正半轴,
∴当x=-1时,y>0,即a-b+c>0.
故本选项正确;
D、由x=2时,y=4a+2b+c,由图象知:y=4a+2b+c>0,故本选项正确;
故选D.
点评:本题考查了二次函数图象与系数的关系.二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
∠A,∠B,∠C是△ABC的三个内角,则sin
等于( )
| A+B |
| 2 |
A、cos
| ||
B、sin
| ||
| C、cosC | ||
D、cos
|
△ABC中,AB=AC,AB的垂直平分线与直线AC相交所成锐角为40°,则此等腰三角形的顶角为( )
| A、50° | B、60° |
| C、130° | D、50°或130° |
两个全等图形中可以不同的是( )
| A、位置 | B、长度 | C、角度 | D、面积 |
下列方程是一元二次方程的是( )
| A、2x+3y=1 | ||
| B、x2=2 | ||
C、x2+
| ||
| D、3x+6=5x+2 |
 已知△ABC,AB边中点为D,E、F分别在AC、BC边上运动,求证:S△DEF≤S△ADE+S△BDF.
已知△ABC,AB边中点为D,E、F分别在AC、BC边上运动,求证:S△DEF≤S△ADE+S△BDF.