题目内容
∠A,∠B,∠C是△ABC的三个内角,则sin
等于( )
| A+B |
| 2 |
A、cos
| ||
B、sin
| ||
| C、cosC | ||
D、cos
|
考点:互余两角三角函数的关系
专题:
分析:利用三角形的内角和得到∴∠A+∠B=180°-∠C,从而得到sin
=sin
=sin(90°-
)=cos
.
| A+B |
| 2 |
| 180°-∠C |
| 2 |
| C |
| 2 |
| C |
| 2 |
解答:解:∵∠A,∠B,∠C是△ABC的三个内角,
∴∠A+∠B+∠C=180°,
∴∠A+∠B=180°-∠C,
∴sin
=sin
=sin(90°-
)=cos
,
故选A.
∴∠A+∠B+∠C=180°,
∴∠A+∠B=180°-∠C,
∴sin
| A+B |
| 2 |
| 180°-∠C |
| 2 |
| C |
| 2 |
| C |
| 2 |
故选A.
点评:考查了互余两角的三角函数的关系及等腰三角形的性质,解题的关键是了解互余的两角之间的关系.

练习册系列答案
相关题目
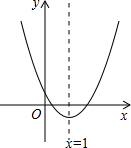 如图,二次函数y=ax2+bx+c图象的对称轴为x=1,则下列说法正确的有( )
如图,二次函数y=ax2+bx+c图象的对称轴为x=1,则下列说法正确的有( )①abc<0,②2a+b=0,③a-b+c>0,④若4a+2b+c>0.
| A、①②③ | B、②③④ |
| C、①②④ | D、①②③④ |
点A为数轴上表示-2的点,将点A向左移4个单位长度到B,点B表示的数是( )
| A、2 | B、-6 |
| C、2或-6 | D、以上都不对 |
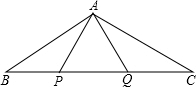 如图,P、Q是△ABC边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC=
如图,P、Q是△ABC边BC上的两点,且BP=PQ=QC=AP=AQ,则∠BAC= 如图:若B,E,C,F在同一条直线上,AB=DF,AC=DE,BE=CF.求证:∠A=∠D.
如图:若B,E,C,F在同一条直线上,AB=DF,AC=DE,BE=CF.求证:∠A=∠D.