题目内容
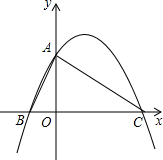 如图,二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点A(0,4),与x轴负半轴交于B,与正半轴交于点C(8,0),且∠BAC=90°.
如图,二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点A(0,4),与x轴负半轴交于B,与正半轴交于点C(8,0),且∠BAC=90°.(1)求该二次函数解析式;
(2)若N是线段BC上一动点,作NE∥AC,交AB于点E,连结AN,当△ANE面积最大时,求点N的坐标;
(3)若点P为x轴上方的抛物线上的一个动点,连接PA、PC,设所得△PAC的面积为S.问:是否存在一个S的值,使得相应的点P有且只有2个?若有,求出这个S的值,并求此时点P的横坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)由射影定理可得出B点坐标,再利用待定系数法求二次函数解析式即可;
(2)利用NE∥AC,则△BNE∽△BAC,得出
=(
)2,由S△ANE=S△BAN-S△ANE,进而利用二次函数最值求法得出即可;
(3)过P作x轴的垂线,交AC于Q,交x轴于H;设出点P的横坐标(设为m),根据抛物线和直线AC的解析式,即可表示出P、Q的纵坐标,从而可得到PQ的长,然后分两种情况进行讨论:
①P点在第一象限时,即0<m<8时,可根据PQ的长以及A、C的坐标,分别表示出△APQ、△CPQ的面积,它们的面积和即为△APC的面积,由此可得到S的表达式,通过配方即可得到S的取值范围;
②当P在第二象限时,即-2<m<0时,同①可求得△APQ、△CPQ的面积,此时它们的面积差为△APC的面积,同理可求得S的取值范围;根据两个S的取值范围,即可判断出所求的结论.
(2)利用NE∥AC,则△BNE∽△BAC,得出
| S△BEN |
| S△BAC |
| BN |
| BC |
(3)过P作x轴的垂线,交AC于Q,交x轴于H;设出点P的横坐标(设为m),根据抛物线和直线AC的解析式,即可表示出P、Q的纵坐标,从而可得到PQ的长,然后分两种情况进行讨论:
①P点在第一象限时,即0<m<8时,可根据PQ的长以及A、C的坐标,分别表示出△APQ、△CPQ的面积,它们的面积和即为△APC的面积,由此可得到S的表达式,通过配方即可得到S的取值范围;
②当P在第二象限时,即-2<m<0时,同①可求得△APQ、△CPQ的面积,此时它们的面积差为△APC的面积,同理可求得S的取值范围;根据两个S的取值范围,即可判断出所求的结论.
解答:解:(1)∵∠BAC=90°,∠AOC=90°,
∴由射影定理可得出:OA2=OB•OC,
由题意知:OA=4,OC=8,
∴42=OB•8,
∴OB=2,
∴B(-2,0),
将A、B、C三点坐标代入即得:
,
解得:
,
∴抛物线解析式为:y=-
x2+
x+4;
(2)设N(n,0),则BN=n+2,BA=10,
∵NE∥AC,
∴△BNE∽△BAC,
∴
=(
)2,
∵S△BAC=
×10×4=20,
∴
=(
)2,
S△BEN=
(n+2)2,
∵S△BAN=
×(n+2)×4=2n+4,
∴S△ANE=(2n+4)-
(n+2)2=-
(n-3)2+5,
∵a=-
,
∴当n=3时,最大值S△ANE=5,
此时N的坐标为:(3,0);
(3)设直线AC对应的函数解析式为:y=kx+b,
则
,
解得:
,
∴直线AC对应的函数解析式为:y=-
x+4,
如图,过P作PH⊥OC,垂足为H,交直线AC于点Q;
设P(m,-
m2+
m+4),则Q(m,-
m+4).
①当0<m<8时,
PQ=(-
m2+
m+4)-(-
m+4)=-
m2+2m,
S=S△APQ+S△CPQ=
×8×(-
m2+2m)=-(m-4)2+16,
∴0<S≤16;
②当-2<m<0时,
PQ=(-
m+4)-(-
m2+
m+4)=
m2-2m,
S=S△CPQ-S△APQ=
×8×(
m2-2m)=(m-4)2-16,
∴0<S<20;
∴当0<S<16时,0<m<8中有m两个值,-2<m<0中m有一个值,此时有三个;
当16<S<20时,-2<m<0中m只有一个值;
当S=16时,m=4或m=4-4
这两个.
故当S=16时,相应的点P有且只有两个.
∴由射影定理可得出:OA2=OB•OC,
由题意知:OA=4,OC=8,
∴42=OB•8,
∴OB=2,
∴B(-2,0),
将A、B、C三点坐标代入即得:
|
解得:
|

∴抛物线解析式为:y=-
| 1 |
| 4 |
| 3 |
| 2 |
(2)设N(n,0),则BN=n+2,BA=10,
∵NE∥AC,
∴△BNE∽△BAC,
∴
| S△BEN |
| S△BAC |
| BN |
| BC |
∵S△BAC=
| 1 |
| 2 |
∴
| S△BEN |
| 20 |
| n+2 |
| 10 |
S△BEN=
| 1 |
| 5 |
∵S△BAN=
| 1 |
| 2 |
∴S△ANE=(2n+4)-
| 1 |
| 5 |
| 1 |
| 5 |
∵a=-
| 1 |
| 5 |
∴当n=3时,最大值S△ANE=5,
此时N的坐标为:(3,0);
(3)设直线AC对应的函数解析式为:y=kx+b,
则
|
解得:
|

∴直线AC对应的函数解析式为:y=-
| 1 |
| 2 |
如图,过P作PH⊥OC,垂足为H,交直线AC于点Q;
设P(m,-
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
①当0<m<8时,
PQ=(-
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
S=S△APQ+S△CPQ=
| 1 |
| 2 |
| 1 |
| 4 |
∴0<S≤16;
②当-2<m<0时,
PQ=(-
| 1 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 4 |
S=S△CPQ-S△APQ=
| 1 |
| 2 |
| 1 |
| 4 |
∴0<S<20;
∴当0<S<16时,0<m<8中有m两个值,-2<m<0中m有一个值,此时有三个;
当16<S<20时,-2<m<0中m只有一个值;
当S=16时,m=4或m=4-4
| 2 |
故当S=16时,相应的点P有且只有两个.
点评:此题考查了二次函数图象与坐标轴交点坐标的求法、图形面积的求法等知识,(3)题的解题过程并不复杂,关键在于理解题意.

练习册系列答案
相关题目
 1300年前,我国隋朝建造的赵州石拱桥是圆弧形,它的跨度AB为37m,高为7m.
1300年前,我国隋朝建造的赵州石拱桥是圆弧形,它的跨度AB为37m,高为7m.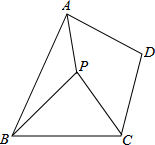 在四边形ABCD中,AB=BC,∠ABC=60°,线段CD绕着点C逆时针旋转60°得到线段CP,连接PA、PB.
在四边形ABCD中,AB=BC,∠ABC=60°,线段CD绕着点C逆时针旋转60°得到线段CP,连接PA、PB.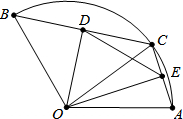 如图,在半径为
如图,在半径为