题目内容
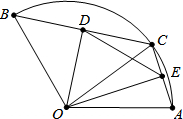
 如图,EG、AF、CB三条直线两两相交,AB、DE分别是∠GAD、∠FDC的角平分线,若AB=AD=DE,则∠DAC=
如图,EG、AF、CB三条直线两两相交,AB、DE分别是∠GAD、∠FDC的角平分线,若AB=AD=DE,则∠DAC=考点:等腰三角形的性质,三角形内角和定理,三角形的外角性质
专题:
分析:设∠DAC=∠1=x°.先由AD=DE,得出∠1=∠2=x°,则∠3=∠1+∠2=2x°,再由角平分线的定义及对顶角的性质得出∠4=∠FDC=4x°,在△ABD中,根据等边对等角的性质及三角形内角和定理得出∠5=180°-∠ABD-∠4=180°-8x°,然后根据平角及角平分线的定义,得到∠1+2∠5=180°,由此列出方程
x+2(180-8x)=180,解方程求出x=12,即∠DAC=12°.
x+2(180-8x)=180,解方程求出x=12,即∠DAC=12°.
解答: 解:如图.设∠DAC=∠1=x°.
解:如图.设∠DAC=∠1=x°.
∵AD=DE,
∴∠1=∠2=x°,
∴∠3=∠1+∠2=2x°.
∵DE是∠FDC的角平分线,
∴∠FDC=2∠3=4x°,
∴∠4=∠FDC=4x°.
在△ABD中,∵AB=AD,
∴∠ABD=∠4=4x°,
∴∠5=180°-∠ABD-∠4=180°-8x°.
∵EG是直线,AB是∠GAD的角平分线,
∴∠1+2∠5=180°,
∴x+2(180-8x)=180,
解得x=12,
即∠DAC=12°.
故答案为12°.
 解:如图.设∠DAC=∠1=x°.
解:如图.设∠DAC=∠1=x°.∵AD=DE,
∴∠1=∠2=x°,
∴∠3=∠1+∠2=2x°.
∵DE是∠FDC的角平分线,
∴∠FDC=2∠3=4x°,
∴∠4=∠FDC=4x°.
在△ABD中,∵AB=AD,
∴∠ABD=∠4=4x°,
∴∠5=180°-∠ABD-∠4=180°-8x°.
∵EG是直线,AB是∠GAD的角平分线,
∴∠1+2∠5=180°,
∴x+2(180-8x)=180,
解得x=12,
即∠DAC=12°.
故答案为12°.
点评:本题考查了等腰三角形等边对等角的性质,三角形内角和定理,角平分线的定义,对顶角的性质,三角形的外角性质,难度适中.设出适当的未知数列出方程是解题的关键.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
观察下列图形(每幅图中最小的三角形都是全等的),请写出第n个图中最小的三角形的个数有( )个.


| A、4n |
| B、3n-2 |
| C、n4 |
| D、4n-1 |
 如图,在半径为
如图,在半径为 2013年12月14日我国的第一艘月球车--“玉兔号”成功软着陆于月球雨海西北部.已知地球与月球之间的平均距离约为380000km,用科学记数法表示地球与月球之间的平均距离约为
2013年12月14日我国的第一艘月球车--“玉兔号”成功软着陆于月球雨海西北部.已知地球与月球之间的平均距离约为380000km,用科学记数法表示地球与月球之间的平均距离约为