题目内容
计算:1+4+7+10+13+16+…+2011+2014.
考点:有理数的加法
专题:
分析:根据后一项加数比前一项加数大3,可得项数,根据等式的性质,可得答案.
解答:解:由后一项加数比前一项加数大3,得
1+3(n-1)=2014,
解得n=672,
设S=1+4+7+10+13+16+…+2011+2014①,
S=2014+2011+2008+…+10+7+4+1②,
①+②得
2S=(1+2014)×672,
S=
=347040.
1+3(n-1)=2014,
解得n=672,
设S=1+4+7+10+13+16+…+2011+2014①,
S=2014+2011+2008+…+10+7+4+1②,
①+②得
2S=(1+2014)×672,
S=
| (1+2014)×672 |
| 2 |
=347040.
点评:本题考查了有理数的加法,先求出加数的个数,再求出和.

练习册系列答案
相关题目
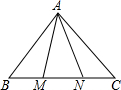 如图,△ABN≌△ACM,AB=AC,BN=CM,∠B=50°,∠ANC=120°,则∠MAC的度数等于( )
如图,△ABN≌△ACM,AB=AC,BN=CM,∠B=50°,∠ANC=120°,则∠MAC的度数等于( )| A、120° | B、70° |
| C、60° | D、50°. |
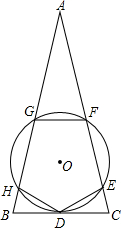 如图,等腰△ABC的顶角∠A=36°.⊙O和底边BC相切于BC的中点D,并与两腰相交于E、F、G、H四点,其中点G、F分别是两腰AB、AC的中点.求证:五边形DEFGH是正五边形.
如图,等腰△ABC的顶角∠A=36°.⊙O和底边BC相切于BC的中点D,并与两腰相交于E、F、G、H四点,其中点G、F分别是两腰AB、AC的中点.求证:五边形DEFGH是正五边形. 如图,在长方形ABCD中,点P从点A开始以2cm/s的速度沿着折线AB-BC-CD向点D移动,若长方形的长AD=6cm,宽AB=4cm,设点P运动的时间为x(s),PB的长为ycm,△PAD的面积为Scm2.
如图,在长方形ABCD中,点P从点A开始以2cm/s的速度沿着折线AB-BC-CD向点D移动,若长方形的长AD=6cm,宽AB=4cm,设点P运动的时间为x(s),PB的长为ycm,△PAD的面积为Scm2.