题目内容
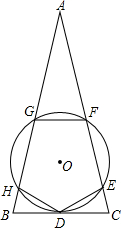 如图,等腰△ABC的顶角∠A=36°.⊙O和底边BC相切于BC的中点D,并与两腰相交于E、F、G、H四点,其中点G、F分别是两腰AB、AC的中点.求证:五边形DEFGH是正五边形.
如图,等腰△ABC的顶角∠A=36°.⊙O和底边BC相切于BC的中点D,并与两腰相交于E、F、G、H四点,其中点G、F分别是两腰AB、AC的中点.求证:五边形DEFGH是正五边形.考点:切线的性质
专题:证明题
分析:连结DF、DG,先证得四边形AFDG是菱形,得出∠BGD=∠FDG=∠CFD=∠A=36°,根据切线的性质得出∠CDE=∠CFD=36°,根据平行线的性质得出∠FDC=∠B=72°,从而求得∠EDF=36°,进而求得∠BGD=∠CFD=∠EFD=∠FDG=∠GDH=36°,根据圆周角的性质得出
=
=
=
=
,即D、E、F、G、H将⊙O五等分,即可证得五边形DEFGH是正五边形.
 |
| HD |
 |
| DE |
 |
| EF |
 |
| FG |
 |
| GH |
解答: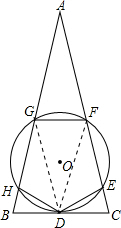 证明:连结DF、DG,
证明:连结DF、DG,
∵G、F分别是两腰AB、AC的中点.D是等腰三角形ABC底边的中线,
∴GD∥AC,GD=AF=
AC,DF∥AB,DF=AG=
AB,
∴四边形AFDG是平行四边形,
∵AB=AC,
∴GD=DF,
∴四边形AFDG是菱形,
∴∠BGD=∠FDG=∠CFD=∠A=36°,
∵BC是切线,
∴∠CDE=∠CFD=36°,
∵DF∥AB,
∴∠FDC=∠B=72°,
∴∠EDF=36°,
同理:∠GDH=36°,
∴∠BGD=∠CFD=∠EFD=∠FDG=∠GDH=36°,
∴
=
=
=
=
,
即D、E、F、G、H将⊙O五等分,
∴五边形DEFGH是正五边形.
 证明:连结DF、DG,
证明:连结DF、DG,∵G、F分别是两腰AB、AC的中点.D是等腰三角形ABC底边的中线,
∴GD∥AC,GD=AF=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形AFDG是平行四边形,
∵AB=AC,
∴GD=DF,
∴四边形AFDG是菱形,
∴∠BGD=∠FDG=∠CFD=∠A=36°,
∵BC是切线,
∴∠CDE=∠CFD=36°,
∵DF∥AB,
∴∠FDC=∠B=72°,
∴∠EDF=36°,
同理:∠GDH=36°,
∴∠BGD=∠CFD=∠EFD=∠FDG=∠GDH=36°,
∴
 |
| HD |
 |
| DE |
 |
| EF |
 |
| FG |
 |
| GH |
即D、E、F、G、H将⊙O五等分,
∴五边形DEFGH是正五边形.
点评:本题考查了圆的切线的性质,圆周角的性质,三角形的中位线的性质,等腰三角形的性质,熟练掌握性质是本题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
计算机网络中有关节点的规定是:有一个总节点下分支出若干支节点,每个支节点下又分支出相同数量的次分支节点,所有的节点都是一台计算机,若在某一局域网络中共有计算机189台,设每个节点下分支出x个支节点,则可列方程为( )
| A、x(1+x)=189 |
| B、1+x+x2=189 |
| C、1+x+x(1+x)=189 |
| D、x(1+x)2=189 |
 如图是由八个全等的等腰直角三角形围成的图形,如果每个等腰直角三角形的直角边长为1,那么小正八边形的边长为
如图是由八个全等的等腰直角三角形围成的图形,如果每个等腰直角三角形的直角边长为1,那么小正八边形的边长为