题目内容
18.如图,已知抛物线y=ax2+c过点(-2,2),(4,5),过定点F(0,2)的直线l:y=kx+2与抛物线交于A、B两点,点B在点A的右侧,过点B作x轴的垂线,垂足为C.(1)求抛物线的解析式;
(2)当点B在抛物线上运动时,判断线段BF与BC的数量关系(>、<、=),并证明你的判断;
(3)P为y轴上一点,以B、C、F、P为顶点的四边形是菱形,设点P(0,m),求自然数m的值;
(4)若k=1,在直线l下方的抛物线上是否存在点Q,使得△QBF的面积最大?若存在,求出点Q的坐标及△QBF的最大面积;若不存在,请说明理由.
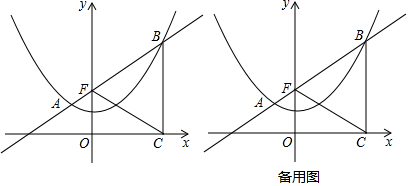
分析 (1)利用待定系数法求抛物线解析式;
(2)设B(x,$\frac{1}{4}$x2+1),而F(0,2),利用两点间的距离公式得到BF2=x2+($\frac{1}{4}$x2+1-2)2=,再利用配方法可得到BF=$\frac{1}{4}$x2+1,由于BC=$\frac{1}{4}$x2+1,所以BF=BC;
(3)如图1,利用菱形的性质得到CB=CF=PF,加上CB=FB,则可判断△BCF为等边三角形,所以∠BCF=60°,则∠OCF=30°,于是可计算出CF=4,所以PF=CF=4,从而得到自然数m的值为6;
(4)作QE∥y轴交AB于E,如图2,先解方程组$\left\{\begin{array}{l}{y=x+2}\\{y=\frac{1}{4}{x}^{2}+1}\end{array}\right.$得B(2+2$\sqrt{2}$,4+2$\sqrt{2}$),设Q(t,$\frac{1}{4}$t2+1),则E(t,t+2),则EQ=-$\frac{1}{4}$t2+t+1,则S△QBF=S△EQF+S△EQB=$\frac{1}{2}$•(2+2$\sqrt{2}$)•EQ=$\frac{1}{2}$•(2+2$\sqrt{2}$)(-$\frac{1}{4}$t2+t+1),然后根据二次函数的性质解决问题.
解答 解:(1)把点(-2,2),(4,5)代入y=ax2+c得$\left\{\begin{array}{l}{4a+c=2}\\{16a+c=5}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{4}}\\{c=1}\end{array}\right.$,
所以抛物线解析式为y=$\frac{1}{4}$x2+1;
(2)BF=BC.
理由如下:
设B(x,$\frac{1}{4}$x2+1),而F(0,2),
∴BF2=x2+($\frac{1}{4}$x2+1-2)2=x2+($\frac{1}{4}$x2-1)2=($\frac{1}{4}$x2+1)2,
∴BF=$\frac{1}{4}$x2+1,
∵BC⊥x轴,
∴BC=$\frac{1}{4}$x2+1,
∴BF=BC;
(3)如图1,m为自然数,则点P在F点上方,
∵以B、C、F、P为顶点的四边形是菱形,
∴CB=CF=PF,
而CB=FB,
∴BC=CF=BF,
∴△BCF为等边三角形,
∴∠BCF=60°,
∴∠OCF=30°,
在Rt△OCF中,CF=2OF=4,
∴PF=CF=4,
∴P(0,6),
即自然数m的值为6;
(4)作QE∥y轴交AB于E,如图2,
当k=1时,一次函数解析式为y=x+2,
解方程组$\left\{\begin{array}{l}{y=x+2}\\{y=\frac{1}{4}{x}^{2}+1}\end{array}\right.$得$\left\{\begin{array}{l}{x=2+2\sqrt{2}}\\{y=4+2\sqrt{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=2-2\sqrt{2}}\\{y=4-2\sqrt{2}}\end{array}\right.$,则B(2+2$\sqrt{2}$,4+2$\sqrt{2}$),
设Q(t,$\frac{1}{4}$t2+1),则E(t,t+2),
∴EQ=t+2-($\frac{1}{4}$t2+1)=-$\frac{1}{4}$t2+t+1,
∴S△QBF=S△EQF+S△EQB=$\frac{1}{2}$•(2+2$\sqrt{2}$)•EQ=($\sqrt{2}$+1)(-$\frac{1}{4}$t2+t+1)=-$\frac{\sqrt{2}+1}{4}$(t-2)2+2$\sqrt{2}$+2
当t=2时,S△QBF有最大值,最大值为2$\sqrt{2}$+2,此时Q点坐标为(2,2).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和菱形的性质;会利用待定系数法求函数解析式;理解坐标与图形性质,记住两点间的距离公式.

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案| A. | 64(x+1)2=50 | B. | 50(x+1)2=64 | C. | 64(1-x)2=50 | D. | 50(1-x)2=64 |
| 年份 | 2014 | 2015 | 2016 | 2017(预计) |
| 快递件总量(亿件) | 140 | 207 | 310 | 450 |
| 电商包裹件(亿件) | 98 | 153 | 235 | 351 |
(2)若2018年“快递件”总量将达到675亿件,请估计其中“电商包裹件”约为多少亿件?
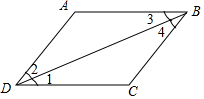 如图,若∠A+∠ABC=180°,则下列结论正确的是( )
如图,若∠A+∠ABC=180°,则下列结论正确的是( )| A. | ∠1=∠2 | B. | ∠2=∠3 | C. | ∠1=∠3 | D. | ∠2=∠4 |
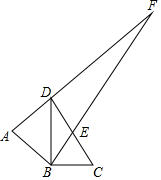 如图,△ABD是以BD为斜边的等腰直角三角形,△BCD中,∠DBC=90°,∠BCD=60°,DC中点为E,AD与BE的延长线交于点F,则∠AFB的度数为( )
如图,△ABD是以BD为斜边的等腰直角三角形,△BCD中,∠DBC=90°,∠BCD=60°,DC中点为E,AD与BE的延长线交于点F,则∠AFB的度数为( )| A. | 30° | B. | 15° | C. | 45° | D. | 25° |
| A. | 3.15×105 | B. | 4.5×105 | C. | 3.15×104 | D. | 4.5×104 |
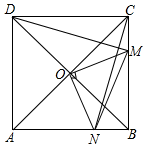 如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列五个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN∽△OAD;④AN2+CM2=MN2;⑤若AB=2,则S△OMN的最小值是$\frac{1}{2}$,其中正确结论的个数是( )
如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列五个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN∽△OAD;④AN2+CM2=MN2;⑤若AB=2,则S△OMN的最小值是$\frac{1}{2}$,其中正确结论的个数是( )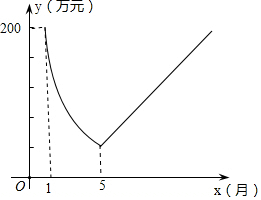 “保护生态环境,建设绿色社会”已经从理念变为人们的行动,某化工厂2016年1月的利润为200万元.设2016年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2016年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).
“保护生态环境,建设绿色社会”已经从理念变为人们的行动,某化工厂2016年1月的利润为200万元.设2016年1月为第1个月,第x个月的利润为y万元.由于排污超标,该厂决定从2016年1月底起适当限产,并投入资金进行治污改造,导致月利润明显下降,从1月到5月,y与x成反比例.到5月底,治污改造工程顺利完工,从这时起,该厂每月的利润比前一个月增加20万元(如图).