题目内容
2.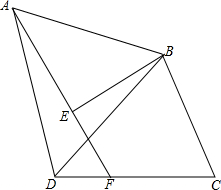 已知等边△ABD中,点E为△ABD内部一点,连接AE、BE,使得∠AEB=90°,过B作BC⊥BE,连接CD,使∠DCB=60°,延长AE交CD于点F,若AE:DC=5:7,且DE•EF=8,则四边形AFCB的面积.
已知等边△ABD中,点E为△ABD内部一点,连接AE、BE,使得∠AEB=90°,过B作BC⊥BE,连接CD,使∠DCB=60°,延长AE交CD于点F,若AE:DC=5:7,且DE•EF=8,则四边形AFCB的面积.
分析 作BG⊥CD,EH⊥CD垂足分别为G、H,连接EG、ED,先证明△ABE≌△DBG得AE=DG,BE=BG,△BEG是等边三角形,设AE=5a用字母a表示出DE、EF,根据DE•EF=8求出a,再代入梯形面积公式即可.
解答 解:如图作BG⊥CD,EH⊥CD垂足分别为G、H,连接EG、ED.
∵EB⊥BC,
∴∠EBC=∠EB=90°,
∴AF∥BC,
∴∠OFD=∠C=60°,
∵∠AOB=∠DOF,∠ABO=∠OFD=60°,
∴∠OAB=∠ODF,
在△ABE和△DBG中,
$\left\{\begin{array}{l}{∠EAB=∠BDG}\\{∠AEB=∠BGD}\\{AB=BD}\end{array}\right.$,
∴△ABE≌△DBG,
∴AE=DG,设AE=5a,则DC=7a,DG=AE=5a,GC=2a,BE=GB=2$\sqrt{3}$a,BC=4a,
∵∠ABE=∠DBG,
∴∠ABD=∠EBG=60°,
∴△EBG是等边三角形,
∴EG=BG=EB=2$\sqrt{3}$a,∠EGB=60°,
在RT△EHG中,∵∠EGH=180°-∠EGB-∠BGC=30°,EG=2$\sqrt{3}$a,
∴EH=$\sqrt{3}a$,GH=3a,DH=2a,HF=a,EF=2a,
DE=$\sqrt{D{H}^{2}+E{H}^{2}}$=$\sqrt{7}$a,
∵DE•EF=8,
∴2a$•\sqrt{7}$a=8,
∴a2=$\frac{4\sqrt{7}}{7}$,
∴S四边形AFCB=$\frac{BC+AF}{2}•BE$=$\frac{7a+4a}{2}•2\sqrt{3}a$=$\frac{44\sqrt{21}}{7}$.
点评 本题考查全等三角形的判定和性质、等边三角形的判定和性质等知识,解题的关键是通过未知数a,想办法表示出相关线段,列出方程解决,本题有点难度.

 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案| A. | 4x-5=3x+2 变形得 4x-3x=2-5 | B. | $\frac{2}{3}$x=$\frac{3}{2}$变形得x=1 | ||
| C. | 3(x-1)=2(x+3)变形得3x-1=2x+6 | D. | $\frac{x-1}{2}$=$\frac{x}{5}$变形得3x=5 |
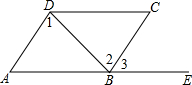 如图,已知AD∥BC,下列结论不一定正确的是( )
如图,已知AD∥BC,下列结论不一定正确的是( )| A. | ∠A+∠ABC=180° | B. | ∠1=∠2 | C. | ∠A=∠3 | D. | ∠C=∠3 |
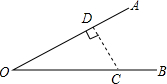 如图,∠O=30°,C为OB上一点,且OC=8,以点C为圆心,半径为4的圆与直线OA的位置关系是( )
如图,∠O=30°,C为OB上一点,且OC=8,以点C为圆心,半径为4的圆与直线OA的位置关系是( )| A. | 相离 | B. | 相交 | ||
| C. | 相切 | D. | 以上三种情况均有可能 |
 已知Rt△ABC中,F、H分别为AB、BC上两点,且AF=BC,BF=HC,求∠HOC度数.
已知Rt△ABC中,F、H分别为AB、BC上两点,且AF=BC,BF=HC,求∠HOC度数. 如图,△ABC中,分别以AB、AC为边向外作正方形ABDE、ACFG.试说明:
如图,△ABC中,分别以AB、AC为边向外作正方形ABDE、ACFG.试说明: