题目内容
7.阅读下列因式分解的过程,再回答问题:1+a+a(1+a)+a(1+a)2=(1+a)[1+a+a(1+a)]=(1+a)2(1+a)=(1+a)3.
(1)上述因式分解的方法是提取公因式.共应用了2次.
(2)若将多项式1+a+a(1+a)+a(1+a)2+…+a(1+a)10分解因式,则可应用上述方法10次,结果是(1+a)11.
(3)分解因式:1+a+a(1+a)+a(1+a)2+…+a(1+a)n(n为正整数).
(4)利用第(3)题的结果计算:1+3+3×4+3×42+…+3×499.
分析 (1)利用观察法可知,用提公因式法提了两次.
(2)因为最后一个式子是(1+a)10,所以需要提10次公因式,结果为(1+a)11.
(3)因为最后一个式子是(1+a)n,所以需要提10次公因式,结果为(1+a)n+1.
(4)利用(3)的结论直接计算即可.
解答 解:(1)上述因式分解的方法是提公因式法.共应用了2次.
故答案分别为:提公因式法,2.
(2)若将多项式1+a+a(1+a)+a(1+a)2+…+a(1+a)10分解因式,则可应用上述方法10次,结果是(1+a)11.
故答案分别为:10,(1+a)11.
(3)原式=(1+a)[1+a+a(1+a)+a(1+a)2+…+a(1+a)n-1]=(1+a)2[1+a+(1+a)+a(1+a)2+…a(1+a)n-2]
=…
=(1+a)n(1+a)
=(1+a)n+1.
(4)原式=(1+3)100=4100.
点评 本题考查提公因式法、解题的关键是找到提公因式的规律,学会用这个方法进行简便计算.

练习册系列答案
相关题目
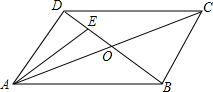 如图,在?ABCD中,对角线AC,BD相交于点O,AC=2AD,点E是OD的中点,连接AE.
如图,在?ABCD中,对角线AC,BD相交于点O,AC=2AD,点E是OD的中点,连接AE.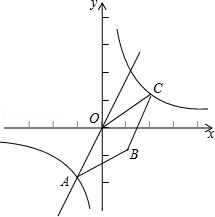 如图,已知正比例函数y=2x和反比例函数y=$\frac{k}{x}$的图象交于点A(m,-2)
如图,已知正比例函数y=2x和反比例函数y=$\frac{k}{x}$的图象交于点A(m,-2)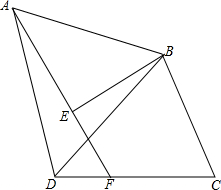 已知等边△ABD中,点E为△ABD内部一点,连接AE、BE,使得∠AEB=90°,过B作BC⊥BE,连接CD,使∠DCB=60°,延长AE交CD于点F,若AE:DC=5:7,且DE•EF=8,则四边形AFCB的面积.
已知等边△ABD中,点E为△ABD内部一点,连接AE、BE,使得∠AEB=90°,过B作BC⊥BE,连接CD,使∠DCB=60°,延长AE交CD于点F,若AE:DC=5:7,且DE•EF=8,则四边形AFCB的面积.