题目内容
6.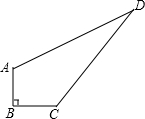 老张家有一块草坪如图所示.家里想整理它,需要知道其面积.老张测量了草坪各边得知:AB=3米,BC=4米,AD=12米,CD=13米,且AB⊥CB.请你帮老张家计算一下这块草坪的面积.
老张家有一块草坪如图所示.家里想整理它,需要知道其面积.老张测量了草坪各边得知:AB=3米,BC=4米,AD=12米,CD=13米,且AB⊥CB.请你帮老张家计算一下这块草坪的面积.
分析 连接AC,根据勾股定理,求得AC,再根据勾股定理的逆定理,判断三角形ACD是直角三角形.这块草坪的面积等于两个直角三角形的面积之和.
解答 解:连接AC,如图,
∵AB⊥BC,
∴∠ABC=90°,
∵AB=3米,BC=4米,
∴AC=5米,
∵CD=12米,DA=13米,
∴AC2+CD2=AD2,
∴△ACD为直角三角形,
∴草坪的面积等于=S△ABC+S△ACD=3×4÷2+5×12÷2=6+30=36(米2).
点评 本题考查了勾股定理和勾股定理的逆定理.在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
相关题目
1.顺次连结对角线互相垂直的四边形各边中点所构成的四边形一定是( )
| A. | 矩形 | B. | 菱形 | C. | 正方形 | D. | 不确定 |
18.已知a方程2x2+3x-4=0的一个根,则代数式2a2+3a的值等于( )
| A. | 4 | B. | 0 | C. | 1 | D. | 2 |
16.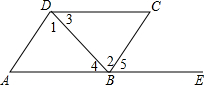 如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
 如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )
如图,点A,B,E在一条直线上,下列条件中不能判断AD∥BC的是( )| A. | ∠1=∠2 | B. | ∠3=∠4 | C. | ∠A=∠5 | D. | ∠A+∠ABC=180° |
 如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点.
如图,在Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,按图中所示方法将△BCD沿BD折叠,使点C落在AB边的C′点.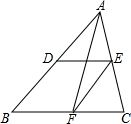 如图,△ABC中,D、E、F分别是AB、AC、BC的中点.若EF=5cm,则AB=10cm;若BC=9cm,则DE=4.5cm;中线AF与DE的关系互相平分.
如图,△ABC中,D、E、F分别是AB、AC、BC的中点.若EF=5cm,则AB=10cm;若BC=9cm,则DE=4.5cm;中线AF与DE的关系互相平分.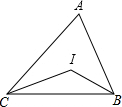 如图,在△ABC,∠ABC和∠ACB的角平分线相交于I,问∠BIC与∠A有什么关系?利用上述关系,计算:
如图,在△ABC,∠ABC和∠ACB的角平分线相交于I,问∠BIC与∠A有什么关系?利用上述关系,计算: