题目内容
【题目】已知关于![]() 的方程
的方程![]()
(1)求证:无论![]() 为何值,方程总有实数根.
为何值,方程总有实数根.
(2)设![]() ,
,![]() 是方程
是方程![]() 的两个根,记
的两个根,记![]() ,S的值能为2吗?若能,求出此时
,S的值能为2吗?若能,求出此时![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
【答案】(1)见解析;(2)![]() 时,S的值为2
时,S的值为2
【解析】
(1)分两种情况讨论:①当k=1时,方程是一元一次方程,有实数根;②当k≠1时,方程是一元二次方程,所以证明判别式是非负数即可;
(2)由韦达定理得![]() ,代入到
,代入到![]() 中,可求得k的值.
中,可求得k的值.
解:(1)①当![]() ,即k=1时,方程为一元一次方程
,即k=1时,方程为一元一次方程![]() ,
,
∴![]() 是方程的一个解.
是方程的一个解.
②当![]() 时,
时,![]() 时,方程为一元二次方程,
时,方程为一元二次方程,
则![]() ,
,
∴方程有两不相等的实数根.
综合①②得,无论k为何值,方程总有实数根.
(2)S的值能为2,根据根与系数的关系可得
![]()
∴![]()
![]() ,
,
即![]() ,解得
,解得![]() ,
,![]()
∵方程有两个根,
∴![]()
∴![]() 应舍去,
应舍去,
∴![]() 时,S的值为2
时,S的值为2

练习册系列答案
相关题目
【题目】某中学开展“唱红歌”比赛活动,九年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示.
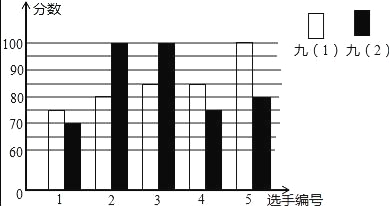
(1)根据图示填写下表:
班级 | 中位数(分) | 众数(分) |
九(1) | 85 | |
九(2) | 100 |
(2)通过计算得知九(2)班的平均成绩为85分,请计算九(1)班的平均成绩.
(3)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩较好.
(4)已知九(1)班复赛成绩的方差是70,请计算九(2)班的复赛成绩的方差,并说明哪个班的成绩比较稳定?