题目内容
11.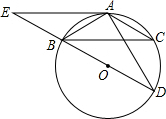 如图,△ABC为⊙O的内接三角形,BD为⊙O的直径,∠ABC=∠D,AC=2$\sqrt{3}$,AD=6,延长DB到E,使BE=BO,连接EA,那么直线EA与⊙O相切吗?为什么?
如图,△ABC为⊙O的内接三角形,BD为⊙O的直径,∠ABC=∠D,AC=2$\sqrt{3}$,AD=6,延长DB到E,使BE=BO,连接EA,那么直线EA与⊙O相切吗?为什么?
分析 先在Rt△ABD中利用勾股定理计算出BD=4$\sqrt{3}$,则OB=OA=2$\sqrt{3}$,证出△OAB为等边三角形,得到∠ABD=∠BAO=60°,再计算出∠BAE=30°,由此得到∠OAE=∠BAO+∠BAE=90°,然后根据切线的判定定理得直线EA与⊙O相切.
解答 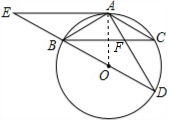 解:直线EA与⊙O相切.
解:直线EA与⊙O相切.
理由如下:连接OA,如图所示:
∵∠ABC=∠D,∠D=∠C,
∴∠ABC=∠C,
∴AB=AC=2$\sqrt{3}$,
Rt△ABD中,∵AB=2$\sqrt{3}$,AD=6,
∴BD=$\sqrt{A{B}^{2}+A{D}^{2}}$=4$\sqrt{3}$,
∴OB=OA=2$\sqrt{3}$,
∴△OAB为等边三角形,
∴∠ABD=∠BAO=60°,
∵BO=BE,
∴BE=AB,
∴∠E=∠BAE,
∴∠BAE=30°,
∴∠OAE=∠BAO+∠BAE=60°+30°=90°,
∴OA⊥AE,
∴直线EA与⊙O相切.
点评 本题考查了圆周角定理、等腰三角形的性质、相似三角形的判定与性质、勾股定理、等边三角形的判定与性质、切线的判定等知识;熟练掌握圆周角定理和勾股定理,证明三角形相似是解决问题的关键.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
16.已知关于x的方程$\frac{a}{x+3}$-$\frac{3}{x+3}$=1的解为负数,且关于x、y的二元一次方程组$\left\{\begin{array}{l}{2x-y=7}\\{3x+y=5a+8}\end{array}\right.$的解之和为正数,则下列各数都满足上述条件a的值的是( )
| A. | $\frac{2}{3}$,2,5 | B. | 0,3,5 | C. | 3,4,5 | D. | 4,5,6 |
 一天皮衣美容店来了一位顾客,要求为他缝补皮大衣上一个三角形的洞,如图所示,店员小李按洞的形状和大小剪下一块毛皮,准备缝制时,发现裁反了.他只好去求助师傅.师傅看后,提示他利用所学的图形知识去考虑,并说只要将三角形皮面再裁成三块,重新拼起来就可以了,这可把小李难住了,聪明的同学们,你能帮助小李解决这个问题吗?
一天皮衣美容店来了一位顾客,要求为他缝补皮大衣上一个三角形的洞,如图所示,店员小李按洞的形状和大小剪下一块毛皮,准备缝制时,发现裁反了.他只好去求助师傅.师傅看后,提示他利用所学的图形知识去考虑,并说只要将三角形皮面再裁成三块,重新拼起来就可以了,这可把小李难住了,聪明的同学们,你能帮助小李解决这个问题吗?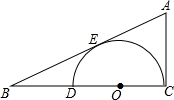 如图,在Rt△ABC中,∠C=Rt∠.D为BC边上一点,以CD为直径作圆O,与AB相切于点E.若CD=2,BD=1.2,求点A到⊙O的切线长.
如图,在Rt△ABC中,∠C=Rt∠.D为BC边上一点,以CD为直径作圆O,与AB相切于点E.若CD=2,BD=1.2,求点A到⊙O的切线长. 如图所示,在⊙O中,已知∠BAC=∠CDA=25°,则∠ABO的度数为40°.
如图所示,在⊙O中,已知∠BAC=∠CDA=25°,则∠ABO的度数为40°.