题目内容
13. 已知实数a,b在数轴上位置如图所示,化简$|a|-\sqrt{b^2}+\sqrt{{{({a-b})}^2}}-\sqrt{4{a^2}}$.
已知实数a,b在数轴上位置如图所示,化简$|a|-\sqrt{b^2}+\sqrt{{{({a-b})}^2}}-\sqrt{4{a^2}}$.
分析 先由数轴上a,b两点的位置,判断出a,b的符号及绝对值的大小,再分别代入各式计算即可.
解答 解:由数轴可得:a<0<b,
∴a-b<0,
|a|-$\sqrt{{b}^{2}}$+$\sqrt{(a-b)^{2}}$-$\sqrt{4{a}^{2}}$=-a-b+|a-b|-|2a|=-a-b-a+b+2a=0.
点评 此题考查了二次根式的化简与性质、绝对值的性质以及实数与数轴的关系.此题难度适中,注意确定a,b之间的大小关系是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.一正多边形外角为90°,则它的边心距与半径之比为( )
| A. | 1:2 | B. | 1:$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | 1:3 |
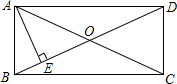 如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠BAE,求∠EAC的度数.
如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠BAE,求∠EAC的度数. 如图,在同一直角坐标系中,作出函数①y=3x2;②y=$\frac{1}{2}{x}^{2}$;③y=x2的图象,则从里到外的三条抛物线对应的函数依次是( )
如图,在同一直角坐标系中,作出函数①y=3x2;②y=$\frac{1}{2}{x}^{2}$;③y=x2的图象,则从里到外的三条抛物线对应的函数依次是( ) 如图,已知△ABC和△AEF都是等边三角形,求证:BF=CE.
如图,已知△ABC和△AEF都是等边三角形,求证:BF=CE.