题目内容
10.已知△ABC∽△A1B1C1的面积比为1:9,则△ABC与△A1B1C1的周长之比为1:3.分析 根据相似三角形面积的比等于相似比的平方,相似三角形周长的比等于相似比进行计算即可.
解答 解:∵△ABC∽△A1B1C1的面积比为1:9,
∴△ABC∽△A1B1C1的相似比为1:9,
∴△ABC与△A1B1C1的周长之比为1:3.
故答案为:1:3.
点评 本题考查对相似三角形性质:相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方;相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.一正多边形外角为90°,则它的边心距与半径之比为( )
| A. | 1:2 | B. | 1:$\sqrt{2}$ | C. | 1:$\sqrt{3}$ | D. | 1:3 |
5. 如图,在同一直角坐标系中,作出函数①y=3x2;②y=$\frac{1}{2}{x}^{2}$;③y=x2的图象,则从里到外的三条抛物线对应的函数依次是( )
如图,在同一直角坐标系中,作出函数①y=3x2;②y=$\frac{1}{2}{x}^{2}$;③y=x2的图象,则从里到外的三条抛物线对应的函数依次是( )
 如图,在同一直角坐标系中,作出函数①y=3x2;②y=$\frac{1}{2}{x}^{2}$;③y=x2的图象,则从里到外的三条抛物线对应的函数依次是( )
如图,在同一直角坐标系中,作出函数①y=3x2;②y=$\frac{1}{2}{x}^{2}$;③y=x2的图象,则从里到外的三条抛物线对应的函数依次是( )| A. | ①②③ | B. | ①③② | C. | ②③① | D. | ③②① |
19.四舍五入得到的近似数0.03050的有效数字有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
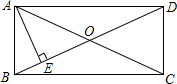 如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠BAE,求∠EAC的度数.
如图,在矩形ABCD中,AE⊥BD于E,∠DAE=3∠BAE,求∠EAC的度数.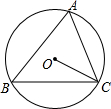 如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为18°.
如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为18°.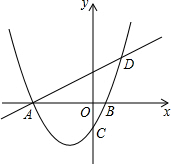 如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,对称轴为直线x=-$\frac{3}{2}$,直线AD交抛物线于点D(2,3).
如图,已知抛物线y=$\frac{1}{2}$x2+bx+c与x轴交于A、B两点,对称轴为直线x=-$\frac{3}{2}$,直线AD交抛物线于点D(2,3).