题目内容
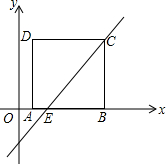 如图,正方形ABCD的顶点A坐标是(1,0),过顶点C的直线y=
如图,正方形ABCD的顶点A坐标是(1,0),过顶点C的直线y=| 4 |
| 3 |
| 8 |
| 3 |
(1)求正方形的边长;
(2)若P是y轴上一点,当PC+PE的值最小时,求P点的坐标.
考点:一次函数综合题
专题:综合题
分析:(1)设点C的坐标为(a,
a-
),则可得OB,根据正方形的四边相等,可得关于a的方程,解出a的值,即可得出正方形的边长;
(2)找点E关于y轴的对称点E′,连接CE′,则CE′与y轴交点,即是点P点的位置,求出CE′解析式,可得点P的坐标.
| 4 |
| 3 |
| 8 |
| 3 |
(2)找点E关于y轴的对称点E′,连接CE′,则CE′与y轴交点,即是点P点的位置,求出CE′解析式,可得点P的坐标.
解答:解:(1)由题意得直线CE解析式为:y=
x-
,
令y=0,可得x=2,
则点E的坐标为(2,0),
设点C的坐标为(a,
a-
),
则AB=OB-OA=a-1,CB=
a-
,
∵四边形ABCD是正方形,
∴AB=CD,
∴a-1=
a-
,
解得:a=5,
则四边形ABCD的边长为4.
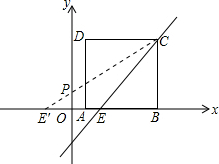
(2)找点E关于y轴的对称点E',连接CE',则CE'与y轴交点,即是点P点的位置,
点E'坐标为(-2,0),
设CE'解析式为y=kx+b,
将点C、E'坐标代入,可得
,
解得:
,
故直线CE'解析式为y=
x+
,
令x=0,则y=
.
即点P的坐标为(0,
).
| 4 |
| 3 |
| 8 |
| 3 |
令y=0,可得x=2,
则点E的坐标为(2,0),
设点C的坐标为(a,
| 4 |
| 3 |
| 8 |
| 3 |
则AB=OB-OA=a-1,CB=
| 4 |
| 3 |
| 8 |
| 3 |
∵四边形ABCD是正方形,
∴AB=CD,
∴a-1=
| 4 |
| 3 |
| 8 |
| 3 |
解得:a=5,
则四边形ABCD的边长为4.
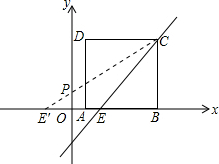
(2)找点E关于y轴的对称点E',连接CE',则CE'与y轴交点,即是点P点的位置,
点E'坐标为(-2,0),
设CE'解析式为y=kx+b,
将点C、E'坐标代入,可得
|
解得:
|
故直线CE'解析式为y=
| 4 |
| 7 |
| 8 |
| 7 |
令x=0,则y=
| 8 |
| 7 |
即点P的坐标为(0,
| 8 |
| 7 |
点评:本题考查了一次函数的综合题,涉及了待定系数法求一次函数解析式、轴对称的性质,解答本题的关键是数形结合思想及待定系数法的应用,难度一般.

练习册系列答案
相关题目
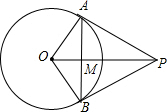 如图,PA、PB是⊙O的切线,切点分别为点A、点B若∠AOB=120°,则下列结论错误的是( )
如图,PA、PB是⊙O的切线,切点分别为点A、点B若∠AOB=120°,则下列结论错误的是( )A、
| ||||
| B、PA=PB | ||||
| C、△PAB是等边三角形 | ||||
D、OM=
|
已知一个多边形的内角和与外角和的比是9:2,则这个多边形的边数是( )
| A、9 | B、10 | C、11 | D、12 |
设n是正整数,则1-(-1)n的值是( )
| A、0或1 | B、1或2 |
| C、0或2 | D、0,1或2 |
已知(5,-1)是双曲线y=
(k≠0)上的一点,则下列各点中不在该图象上的是( )
| k |
| x |
A、(
| ||
| B、(5,1) | ||
| C、(-1,5) | ||
D、(10,-
|
下列计算正确的是( )
A、
| ||||||||
B、
| ||||||||
C、5
| ||||||||
D、2
|
方程(x-4)(x+3)=0的根是( )
| A、x1=-4,x2=3 |
| B、x1=4,x2=3 |
| C、x1=4,x2=-3 |
| D、x1=-4,x2=-3 |
