题目内容
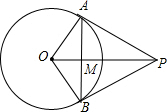 如图,PA、PB是⊙O的切线,切点分别为点A、点B若∠AOB=120°,则下列结论错误的是( )
如图,PA、PB是⊙O的切线,切点分别为点A、点B若∠AOB=120°,则下列结论错误的是( )A、
| ||||
| B、PA=PB | ||||
| C、△PAB是等边三角形 | ||||
D、OM=
|
考点:切线的性质
专题:
分析:根据切线长定理得到PA=PB,OP平分∠APB,根据切线的性质得∠OAP=∠OBP=90°,再利用四边形的内角和得到∠APB=180°-∠AOB=60°,于是可判断△PAB为等边三角形;
则OP⊥AB,根据垂径定理得到
=
;然后计算出∠OAM=30°,则根据含30度的直角三角形三边的关系得到OM=
OA.
则OP⊥AB,根据垂径定理得到
 |
| AN |
 |
| BN |
| 1 |
| 2 |
解答:解:OP与⊙O相交于N,如图,
∵PA、PB是⊙O的切线,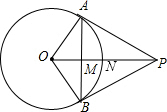
∴PA=PB,OA⊥PA,OB⊥PB,OP平分∠APB,
∴∠OAP=∠OBP=90°,
∴∠APB=180°-∠AOB=180°-120°=60°,
∴△PAB为等边三角形;
∴OP⊥AB,
∴
=
;
∵∠PAM=60°,
∴∠OAM=30°,
∴OM=
OA.
故选A.
∵PA、PB是⊙O的切线,

∴PA=PB,OA⊥PA,OB⊥PB,OP平分∠APB,
∴∠OAP=∠OBP=90°,
∴∠APB=180°-∠AOB=180°-120°=60°,
∴△PAB为等边三角形;
∴OP⊥AB,
∴
 |
| AN |
 |
| BN |
∵∠PAM=60°,
∴∠OAM=30°,
∴OM=
| 1 |
| 2 |
故选A.
点评:本题考查了切线的性质:圆的切线垂直于经过切点的半径.若出现圆的切线,必连过切点的半径,构造定理图,得出垂直关系.

练习册系列答案
相关题目
已知x:y=5:2,则下列各式中不正确的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
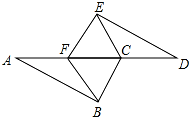 如图,已知AB∥DE,AB=DE,AF=DC,请问图中有
如图,已知AB∥DE,AB=DE,AF=DC,请问图中有 如图所示,在Rt△ABC中,∠C=90°,D是AC边上一点,AB=5,AC=4,若△ABC与△BDC相似,求CD的长.
如图所示,在Rt△ABC中,∠C=90°,D是AC边上一点,AB=5,AC=4,若△ABC与△BDC相似,求CD的长.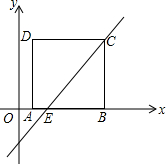 如图,正方形ABCD的顶点A坐标是(1,0),过顶点C的直线y=
如图,正方形ABCD的顶点A坐标是(1,0),过顶点C的直线y=