题目内容
19. 如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有3对全等三角形.
如图,OP平分∠MON,PE⊥OM于E,PF⊥ON于F,OA=OB,则图中有3对全等三角形.
分析 由OP平分∠MON,PE⊥OM于E,PF⊥ON于F,得到PE=PF,∠1=∠2,证得△AOP≌△BOP,再根据△AOP≌△BOP,得出AP=BP,于是证得△AOP≌△BOP,和Rt△AOP≌Rt△BOP.
解答  解:OP平分∠MON,PE⊥OM于E,PF⊥ON于F,
解:OP平分∠MON,PE⊥OM于E,PF⊥ON于F,
∴PE=PF,∠1=∠2,
在△AOP与△BOP中,
$\left\{\begin{array}{l}{OA=OB}\\{∠1=∠2}\\{OP=OP}\end{array}\right.$,
∴△AOP≌△BOP,
∴AP=BP,
在△EOP与△FOP中,
$\left\{\begin{array}{l}{∠1=∠2}\\{∠OEP=∠OFP=90°}\\{OP=OP}\end{array}\right.$,
∴△EOP≌△FOP,
在Rt△AEP与Rt△BFP中,
$\left\{\begin{array}{l}{PA=PB}\\{PE=PF}\end{array}\right.$,
∴Rt△AEP≌Rt△BFP,
∴图中有3对全等三角形,
故答案为:3.
点评 本题考查了角平分线的性质,全等三角形的判定和性质,熟练掌握全等三角形的判定定理是解题的关键.

练习册系列答案
相关题目
14.2015年初,一列CRH5型高速车组进行了“300000公里正线运营考核”标志着中国高速快车从“中国制造”到“中国创造”的飞跃,将300000用科学记数法表示为( )
| A. | 3×106 | B. | 3×105 | C. | 0.3×106 | D. | 30×104 |
11.丽华根据演讲比赛中九位评委所给的分数作了如下表格:
如果去掉一个最高分和一个最低分,则表中数据一定不发生变化的是( )
| 平均数 | 中位数 | 众数 | 方差 |
| 8.5 | 8.3 | 8.1 | 0.15 |
| A. | 平均数 | B. | 众数 | C. | 方差 | D. | 中位数 |
8.色盲是伴X染色体隐性先天遗传病,患者中男性远多于女性,从男性体检信息库中随机抽取体检表,统计结果如表:
根据表中数据,估计在男性中,男性患色盲的概率为0.07(结果精确到0.01)
| 抽取的体检表数n | 50 | 100 | 200 | 400 | 500 | 800 | 1000 | 1200 | 1500 | 2000 |
| 色盲患者的频数m | 3 | 7 | 13 | 29 | 37 | 55 | 69 | 85 | 105 | 138 |
| 色盲患者的频率m/n | 0.060 | 0.070 | 0.065 | 0.073 | 0.074 | 0.069 | 0.069 | 0.071 | 0.070 | 0.069 |
9.二次函数y=x2+x+c的图象与x轴的两个交点A(x1,0),B(x2,0),且x1<x2,点P(m,n)是图象上一点,那么下列判断正确的是( )
| A. | 当n<0时,m<0 | B. | 当n>0时,m>x2 | C. | 当n<0时,x1<m<x2 | D. | 当n>0时,m<x1 |
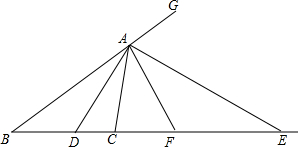 如图,已知△ABC中,AD,AE分别是∠CAB及其外角平分线,分别交CB及CB的延长线于D、E,F为DE的中点,求证:
如图,已知△ABC中,AD,AE分别是∠CAB及其外角平分线,分别交CB及CB的延长线于D、E,F为DE的中点,求证: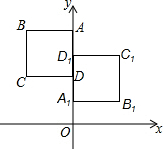 如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).
如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1,D三点的坐标分别是(0,4),(0,3),(0,2).