题目内容
18.已知,点O在直线DE上,AO⊥BO,OC⊥DE,∠COB=50°,求:∠AOC,∠DOC和∠A0E的度数.分析 根据垂直的定义,可得∠DOC=∠AOB=∠COE=90°,根据角的和差,可得答案.
解答 解:如图: ,
,
AO⊥BO,OC⊥DE,
∠DOC=∠AOB=∠COE=90°,
由∠COB=50°得:
∠AOC=∠AOB-∠BOC=90°-50°=40°,
∠AOE=∠AOC+∠COE=40°+90°=130°.
点评 本题考查了垂线,利用了垂线的定义,角的和差.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
13.x表示一个两位数,y表示一个三位数,如果把x放在y的左边组成一个五位数,那么这个五位数就可以表示为( )
| A. | xy | B. | x+y | C. | 1 000x+y | D. | 10x+y |
3.对抛物线y=-x2+2x-3而言,下列结论正确的是( )
| A. | 与x轴有两个交点 | B. | 顶点坐标是(1,-2) | ||
| C. | 与y轴的交点坐标是(0,3) | D. | 开口向上 |
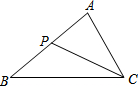 如图,P是△ABC的边AB上一点,请添加一个条件使得△ABC与△ACP相似,则你添加的条件可以是∠B=∠ACP.(只需添加一个符合的条件即可)
如图,P是△ABC的边AB上一点,请添加一个条件使得△ABC与△ACP相似,则你添加的条件可以是∠B=∠ACP.(只需添加一个符合的条件即可)