题目内容
(1)若x1,x2是方程x2+px+q=0的两个根,其中p2-4q≥0,求证:x1+x2=-p,x1•x2=q;
(2)若抛物线y=x2+px+p-2与x轴交于点A(x1,0)和B(x2,0)(x2>x1),设线段AB的长为d,当p为何值时,d2有最小值?并求出最小值.
(2)若抛物线y=x2+px+p-2与x轴交于点A(x1,0)和B(x2,0)(x2>x1),设线段AB的长为d,当p为何值时,d2有最小值?并求出最小值.
考点:抛物线与x轴的交点,根与系数的关系
专题:
分析:(1)先根据求根公式得出x1、x2的值,再求出两根的和与积即可;
(2)由d=|x1-x2|可知d2=(x1-x2)2=(x1+x2)2-4 x1•x2=p2,再由(1)中 x1+x2=-p,x1•x2=q即可得出结论.
(2)由d=|x1-x2|可知d2=(x1-x2)2=(x1+x2)2-4 x1•x2=p2,再由(1)中 x1+x2=-p,x1•x2=q即可得出结论.
解答:(1)证明:∵方程x2+px+q=0的两个根为x1=
,x2=
.
∴x1+x2=
+
=-p,
x1•x2=
×
q;
(2)解:由(1)得,x1+x2=-p,x1•x2=p-2,
∴d2=(x2-x1)2=(x1+x2)2-4x1x2=p2-4(p-2),
即d2=p2-4p+8=(p-2)2+4,
∴当p=2时,d2有最小值,最小值为4.
-p+
| ||
| 2 |
-p-
| ||
| 2 |
∴x1+x2=
-p+
| ||
| 2 |
-p-
| ||
| 2 |
x1•x2=
-p+
| ||
| 2 |
-p-
| ||
| 2 |
(2)解:由(1)得,x1+x2=-p,x1•x2=p-2,
∴d2=(x2-x1)2=(x1+x2)2-4x1x2=p2-4(p-2),
即d2=p2-4p+8=(p-2)2+4,
∴当p=2时,d2有最小值,最小值为4.
点评:本题考查的是抛物线与x轴的交点及根与系数的关系,熟知x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q是解答此题的关键.

练习册系列答案
相关题目
面积为16cm2的正方形,对角线的长为( )cm.
| A、4 | ||
B、4
| ||
| C、8 | ||
D、8
|
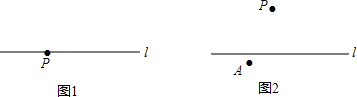 我们知道“经过一点有且只有一条直线与已知直线垂直”,那么如何用(不带刻度)直尺和圆规来作图呢?
我们知道“经过一点有且只有一条直线与已知直线垂直”,那么如何用(不带刻度)直尺和圆规来作图呢? 如图,已知△ABC.
如图,已知△ABC.