题目内容
现用边长相等且边数分别为a、b、c、d(边数不全相等)的四种正多边形刚好能进行平面镶嵌,则
+
+
+
=( )
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| d |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
考点:平面镶嵌(密铺)
专题:
分析:先根据四种正多边形刚好能进行平面镶嵌,得出
+
+
+
=360°,再进行整理即可.
| (a-2)180° |
| a |
| (b-2)180° |
| b |
| (c-2)180° |
| c |
| (d-2)180° |
| d |
解答:解;∵四种正多边形刚好能进行平面镶嵌,
∴
+
+
+
=360°,
∴
+
+
+
=2,
∴
+
+
+
=1,
故选;A.
∴
| (a-2)180° |
| a |
| (b-2)180° |
| b |
| (c-2)180° |
| c |
| (d-2)180° |
| d |
∴
| a-2 |
| a |
| b-2 |
| b |
| c-2 |
| c |
| d-2 |
| d |
∴
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 1 |
| d |
故选;A.
点评:本题主要考查组成平面镶嵌的条件及多边形的内角和定理,关键是根据组成平面镶嵌的条件,列出的算式并进行整理变形.

练习册系列答案
相关题目
 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠J=( )
如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I+∠J=( )| A、180° | B、360° |
| C、540° | D、720° |
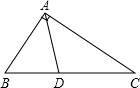 如图,△ABC中,∠BAC=90°,∠B=2∠C,D点在BC上,AD平分∠BAC,若AB=1,则BD的长为( )
如图,△ABC中,∠BAC=90°,∠B=2∠C,D点在BC上,AD平分∠BAC,若AB=1,则BD的长为( )A、
| ||
B、2
| ||
C、
| ||
D、2
|
 如图,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B,C.若∠A=40°,则∠ABX+∠ACX=( )
如图,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B,C.若∠A=40°,则∠ABX+∠ACX=( )| A、25° | B、30° |
| C、45° | D、50° |
 已知:如图,△ABC中,∠ABC=60°,∠ACB=80°,延长CB至D,使BD=BA,延长BC至E,使CE=CA,连结AD、AE,则∠DAE的度数是( )
已知:如图,△ABC中,∠ABC=60°,∠ACB=80°,延长CB至D,使BD=BA,延长BC至E,使CE=CA,连结AD、AE,则∠DAE的度数是( )| A、90° | B、100° |
| C、110° | D、120° |
 ∠A=20°,AB=BC=CD=DE=EF,则∠CDE等于
∠A=20°,AB=BC=CD=DE=EF,则∠CDE等于