题目内容
三个同心圆的半径分别为r1、r2、r3,且r1<r2<r3,如果大圆的面积被两个小圆分成面积相等的三部分,则r1?r2?r3为
- A.1:2:3
- B.

- C.1:4:9
- D.
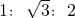
B
分析:这三个面积分别为两个圆环和一个圆的面积,用半径表示出这三个面积,即可表示出三个半径的比.
解答:根据题意可知大圆的面积被两个小圆分成面积相等的三部分,所以πr12=πr22-πr12=πr32-πr22;所以r12:r22:r32=1:2:3;则r1?r2?r3= ,故选B.
,故选B.
点评:主要考查了同心圆中圆环的面积求法.注意掌握其方法是大圆面积减去小圆面积可求解.
分析:这三个面积分别为两个圆环和一个圆的面积,用半径表示出这三个面积,即可表示出三个半径的比.
解答:根据题意可知大圆的面积被两个小圆分成面积相等的三部分,所以πr12=πr22-πr12=πr32-πr22;所以r12:r22:r32=1:2:3;则r1?r2?r3=
 ,故选B.
,故选B.点评:主要考查了同心圆中圆环的面积求法.注意掌握其方法是大圆面积减去小圆面积可求解.

练习册系列答案
相关题目
三个同心圆的半径分别为r1、r2、r3,且r1<r2<r3,如果大圆的面积被两个小圆分成面积相等的三部分,则r1?r2?r3为( )
| A、1:2:3 | ||||
B、1:
| ||||
| C、1:4:9 | ||||
D、1:
|
设三个同心圆的半径分别为r1、r2、r3,且r1>r2>r3,如果大圆的面积被两个小圆分成面积相等的三部分,那么r1:r2:r3为( )
| A、3:2:1 | ||||
| B、9:4:1 | ||||
C、2:
| ||||
D、
|
 :1
:1 :
: :1
:1