题目内容
6.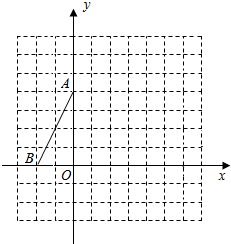 如图,在平面直角坐标系中,O是坐标原点,点A、B的坐标分别为A(0,4)和B(-2,0),连结AB.
如图,在平面直角坐标系中,O是坐标原点,点A、B的坐标分别为A(0,4)和B(-2,0),连结AB.(1)现将△AOB绕点A按逆时针方向旋转90°得到△AO1B1,请画出△AO1B1,并直接写出点B1、O1的坐标(注:不要求证明);
(2)求经过B、A、O1三点的抛物线对应的函数关系式,并画出抛物线的略图.
分析 (1)利用旋转的性质作出B和O旋转后的对应点,即可作出直角三角形;
(2)首先利用待定系数法求得函数的额解析式,然后根据抛物线过A、B和O1即可作出抛物线.
解答 解:(1)如图,画出△AO1B1;
B1(4,2),O1(4,4);
(2)设所求抛物线对应的函数关系式为y=a(x-m)2+n,
由AO1∥x轴,得 m=2.
∴y=a(x-2)2+n.
∵抛物线经过点A、B,
∴$\left\{\begin{array}{l}4a+n=4\;\\ 16a+n=0\;.\end{array}\right.$,
解得$\left\{\begin{array}{l}a=-\frac{1}{3}\;\\ n=\frac{16}{3}\;.\end{array}\right.$.
∴所求抛物线对应的函数关系式为$y=-\frac{1}{3}{(x-2)^2}+\frac{16}{3}$,
即$y=-\frac{1}{3}{x^2}+\frac{4}{3}x+4$,
所画抛物线图象如图所示. .
.
点评 本题考查了旋转作图以及待定系数法求函数的解析式,正确求得函数的解析式是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20. 在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证等式( )
在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证等式( )
 在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证等式( )
在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证等式( )| A. | (a+b)2=a2+2ab+b2 | B. | (a-b)2=a2-2ab+b2 | ||
| C. | a2-b2=(a+b)(a-b) | D. | (a+b)(a-2b)=a2-ab-2b2 |
18.下列是同类项的是( )
| A. | 3xy与xy2 | B. | -2a与a | C. | -3m与mn | D. | $\frac{1}{3}$a2b与b2a |
16.今年铁路大提速,小明的爸爸因要出差,于是去火车站查询列车的开行时间.下面是小明的爸爸从火车站带回家的最新时刻表:
小明的爸爸找出以前同一车次的时刻表如下:
比较了两张时刻表后,小明的爸爸提出了如下问题,请你帮小明解答:
(1)请直接写出现在该次列车的运行时间是多少小时?
(2)现在该次列车的运行时间比以前缩短了多少小时?
(3)若该次列车提速后的平均时速为每小时200千米,那么,该次列车原来的平均时速为多少?(结果精确到个位)
| 2015年10月18日起1008次列车时刻表 | |||
| 始发点 | 发车时间 | 终点站 | 到站时间 |
| A站 | 上午8:20 | B站 | 次日12:20 |
| 2014年1008次列车时刻表 | |||
| 始发点 | 发车时间 | 终点站 | 到站时间 |
| A站 | 下午14:30 | B站 | 第三日8:30 |
(1)请直接写出现在该次列车的运行时间是多少小时?
(2)现在该次列车的运行时间比以前缩短了多少小时?
(3)若该次列车提速后的平均时速为每小时200千米,那么,该次列车原来的平均时速为多少?(结果精确到个位)
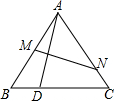 如图,点M、N分别是等边三角形ABC中AB,AC边上的点,点A关于MN的对称点落在BC边上的点D处.若$\frac{BD}{DC}$=$\frac{2}{3}$,则$\frac{AM}{AN}$的值$\frac{7}{8}$.
如图,点M、N分别是等边三角形ABC中AB,AC边上的点,点A关于MN的对称点落在BC边上的点D处.若$\frac{BD}{DC}$=$\frac{2}{3}$,则$\frac{AM}{AN}$的值$\frac{7}{8}$.
 如图,一次函数y=-x+4的图象与x轴、y轴分别相交于点A、B,过点A作x轴的垂线l,点P为直线l上的动点,点Q为直线AB与△OAP外接圆的交点,点P、Q与点A都不重合.
如图,一次函数y=-x+4的图象与x轴、y轴分别相交于点A、B,过点A作x轴的垂线l,点P为直线l上的动点,点Q为直线AB与△OAP外接圆的交点,点P、Q与点A都不重合.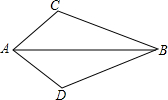 如图,∠C=∠D,AC=AD,求证:BC=BD.
如图,∠C=∠D,AC=AD,求证:BC=BD.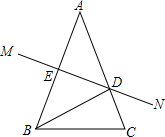 已知:如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
已知:如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.