题目内容
如图，AB是⊙O的弦，半径OA=2，弦AB的长是2| 3 |
| A、100° | B、120° |
| C、130° | D、150° |
考点：垂径定理,特殊角的三角函数值
专题：计算题
分析：作OC⊥AB于C，根据垂径定理得AC=
AB=
，在Rt△AOC中，利用正弦的定义得sinA=
=
，根据特殊角的三角函数值得∠A=30°，然后根据等腰三角形的性质和三角形内角和定理求∠A的度数．
| 1 |
| 2 |
| 3 |
| OC |
| OA |
| 1 |
| 2 |
解答：
解：作OC⊥AB于C，如图，
∵OC⊥AB，
∴AC=BC=
AB=
×2
=
，
在Rt△AOC中，OA=2，
∴sinA=
=
，
∴∠A=30°，
∵OA=OB，
∴∠B=∠A=30°，
∴∠AOB=180°-30°-30°=120°．
故选B．
解：作OC⊥AB于C，如图，∵OC⊥AB，
∴AC=BC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
在Rt△AOC中，OA=2，
∴sinA=
| OC |
| OA |
| 1 |
| 2 |
∴∠A=30°，
∵OA=OB，
∴∠B=∠A=30°，
∴∠AOB=180°-30°-30°=120°．
故选B．
点评：本题考查了垂径定理：平分弦的直径平分这条弦，并且平分弦所对的两条弧．也考查了勾股定理和特殊角的三角函数值．
练习册系列答案
相关题目
如图，BD是⊙O的直径，A是BD延长线上的一点，AC切⊙O于E，CB⊥AB于B，若AE：EC=2：1，DE+BE=4+2
如图所示是一种“羊头”形图案，其作法是：从正方形①开始，以它的一条边为斜边，向外作等腰三角形，然后再以其直角边为边，分别向外作正方形②和②′，…，依此类推，若正方形⑦的边长为1cm，则正方形①的边长下列语句不是命题的是（ ）
| A、画两个相等的角 |
| B、2是一个偶数 |
| C、等边三角形是特殊的等腰三角形 |
| D、直角小于锐角 |
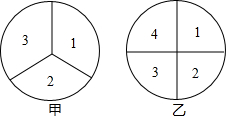如图是两个可以自由转动的转盘，甲转盘被等分成3个扇形，乙转盘被等分成4个扇形，每一个扇形上都标有相应的数字，小军和小亮利用它们做游戏，游戏规则是：同时转动两个转盘，当转盘停止后，转盘甲所指数字作为被除数，转盘乙所指数字作为除数，如果商大于1，小军获胜，否则小亮获胜，（当指针恰好停在分格线上时视为无效，重转）．