题目内容
某工厂共有10台机器,生产一种仪器元件,由于受生产能力和技术水平等因素限制,会产生一定数量的次品.每台机器产生的次品数p(千件)与每台机器的日产量x(千件)(生产条件要求4≤x≤12)之间变化关系如表:
已知每生产1千件合格的元件可以盈利1.6千元,但没生产1千件次品将亏损0.4千元.(利润=盈利-亏损)
(1)观察并分析表中p与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识求出p(千件)与x(千件)的函数解析式;
(2)设该工厂每天生产这种元件所获得的利润为y(千元),试将y表示x的函数;并求当每台机器的日产量x(千件)为多少时所获得的利润最大,最大利润为多少?
| 日产量x(千件/台) | … | 5 | 6 | 7 | 8 | 9 | … |
| 次品数p(千件/台) | … | 0.7 | 0.6 | 0.7 | 1 | 1.5 | … |
(1)观察并分析表中p与x之间的对应关系,用所学过的一次函数,反比例函数或二次函数的有关知识求出p(千件)与x(千件)的函数解析式;
(2)设该工厂每天生产这种元件所获得的利润为y(千元),试将y表示x的函数;并求当每台机器的日产量x(千件)为多少时所获得的利润最大,最大利润为多少?
考点:二次函数的应用
专题:
分析:(1)由表格中的数据可以看出p与x是二次函数关系,根据对称点找出顶点坐标(6,0.6),设出顶点式代入点求得函数即可;
(2)根据实际利润=合格产品的盈利-生产次品的亏损将生产这种元件所获得的实际利润y(万元) 表示为日产量x(万件)的函数;再进一步求得最值即可.
(2)根据实际利润=合格产品的盈利-生产次品的亏损将生产这种元件所获得的实际利润y(万元) 表示为日产量x(万件)的函数;再进一步求得最值即可.
解答:解:(1)根据表格中的数据可以得出:p与x是二次函数关系,且图象经过的顶点坐标为(6,0.6),
设函数解析式为p=a(x-6)2+0.6,把(8,1)代入,的
4a+0.6=1
解得a=0.1,
所以函数解析式为p=0.1(x-6)2+0.6=0.1x2-1.2x+4.2;
(2)y=10[1.6(x-p)-0.4p]
=16x-20p
=16x-20(0.1x2-1.2x+4.2)
=-2x2+40x-84(4≤x≤12)
y=-2x2+40x-84
=-2(x-10)2+116,
∵4≤x≤12
∴当x=10时,y取得最大值,最大利润为116千元
答:当每台机器的日产量为10千件时,所获得的利润最大,最大利润为116千元.
设函数解析式为p=a(x-6)2+0.6,把(8,1)代入,的
4a+0.6=1
解得a=0.1,
所以函数解析式为p=0.1(x-6)2+0.6=0.1x2-1.2x+4.2;
(2)y=10[1.6(x-p)-0.4p]
=16x-20p
=16x-20(0.1x2-1.2x+4.2)
=-2x2+40x-84(4≤x≤12)
y=-2x2+40x-84
=-2(x-10)2+116,
∵4≤x≤12
∴当x=10时,y取得最大值,最大利润为116千元
答:当每台机器的日产量为10千件时,所获得的利润最大,最大利润为116千元.
点评:此题考查的知识点是根据实际问题选择函数类型,熟练掌握二次函数的图象和性质是解答的关键.

练习册系列答案
相关题目
 如图,AB是⊙O的弦,半径OA=2,弦AB的长是2
如图,AB是⊙O的弦,半径OA=2,弦AB的长是2| 3 |
| A、100° | B、120° |
| C、130° | D、150° |
 力龙羽毛球商场经理对新进某一品牌几种号码的男式羽毛球鞋的销售情况进行了一周的统计,得到一组数据后,绘制了频数、频率统计表与频数分布直方图如图所示:
力龙羽毛球商场经理对新进某一品牌几种号码的男式羽毛球鞋的销售情况进行了一周的统计,得到一组数据后,绘制了频数、频率统计表与频数分布直方图如图所示:
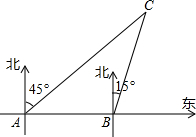 钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持40海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C.
钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持40海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C.