题目内容
4. 在直角坐标系中,直线y=x+1与y轴交于点A,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C3C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…Sn,则Sn的值为22n-3(用含n的代数式表示,n为正整数).
在直角坐标系中,直线y=x+1与y轴交于点A,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C3C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…Sn,则Sn的值为22n-3(用含n的代数式表示,n为正整数).
分析 根据直线解析式先求出OA1=1,得出第一个正方形的边长为1,求得A2B1=A1B1=1,再求出第二个正方形的边长为2,求得A3B2=A2B2=2,第三个正方形的边长为22,求得A4B3=A3B3=22,得出规律,根据三角形的面积公式即可求出Sn的值.
解答 方法一:
解:∵直线y=x+1,当x=0时,y=1,当y=0时,x=-1,
∴OA1=1,OD=1,
∴∠ODA1=45°,
∴∠A2A1B1=45°,
∴A2B1=A1B1=1,
∴S1=$\frac{1}{2}$×1×1=$\frac{1}{2}$,
∵A2B1=A1B1=1,
∴A2C1=2=21,
∴S2=$\frac{1}{2}$×(21)2=21
同理得:A3C2=4=22,…,
S3=$\frac{1}{2}$×(22)2=23
∴Sn=$\frac{1}{2}$×(2n-1)2=22n-3
故答案为:22n-3.
方法二:
∵y=x+1,正方形A1B1C1O,
∴OA1=OC1=1,A2C1=2,B1C1=1,
∴A2B1=1,S1=$\frac{1}{2}$,
∵OC2=1+2=3,
∴A3C2=4,B2C2=2,
∴A3B2=2,
S2=2,
∴q=$\frac{2}{\frac{1}{2}}$=4,
∴Sn=$\frac{1}{2}×{4}^{n-1}={2}^{2n-3}$.
点评 本题考查了一次函数图象上点的坐标特征以及正方形的性质;通过求出第一个正方形、第二个正方形和第三个正方形的边长得出规律是解决问题的关键.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
19.下列命题正确的是( )
| A. | 矩形的对角线互相垂直 | |
| B. | 两边和一角对应相等的两个三角形全等 | |
| C. | 分式方程$\frac{x-2}{2x-1}$+1=$\frac{1.5}{1-2x}$可化为一元一次方程x-2+(2x-1)=-1.5 | |
| D. | 多项式t2-16+3t因式分解为(t+4)(t-4)+3t |
16.一组数据6、4、a、3、2的平均数是4,则这组数据的方差为( )
| A. | 0 | B. | 2 | C. | $\sqrt{2}$ | D. | 10 |
13.在以下数据75,80,80,85,90中,众数、中位数分别是( )
| A. | 75,80 | B. | 80,80 | C. | 80,85 | D. | 80,90 |
14.下列运算结果正确的是( )
| A. | -87×(-83)=7221 | B. | -2.68-7.42=-10 | C. | 3.77-7.11=-4.66 | D. | $\frac{-101}{102}<\frac{-102}{103}$ |
 如图,矩形OABC的顶点A、C的坐标分别是(4,0)和(0,2),反比例函数y=$\frac{k}{x}$(x>0)的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为$\frac{15}{4}$.
如图,矩形OABC的顶点A、C的坐标分别是(4,0)和(0,2),反比例函数y=$\frac{k}{x}$(x>0)的图象过对角线的交点P并且与AB,BC分别交于D,E两点,连接OD,OE,DE,则△ODE的面积为$\frac{15}{4}$.
 如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长是6.
如图,菱形ABCD的边长为6,∠ABC=60°,则对角线AC的长是6.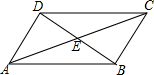 如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( )
如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( )