题目内容
9．
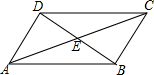如图，在四边形ABCD中，对角线AC，BD相交于点E，∠CBD=90°，BC=4，BE=ED=3，AC=10，则四边形ABCD的面积为（ ）| A． | 6 | B． | 12 | C． | 20 | D． | 24 |
分析 根据勾股定理，可得EC的长，根据平行四边形的判定，可得四边形ABCD的形状，根据平行四边形的面积公式，可得答案．
解答 解：在Rt△BCE中，由勾股定理，得
CE=$\sqrt{B{C}^{2}+B{E}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5．
∵BE=DE=3，AE=CE=5，
∴四边形ABCD是平行四边形．
四边形ABCD的面积为BC•BD=4×（3+3）=24，
故选：D．
点评 本题考查了平行四边形的判定与性质，利用了勾股定理得出CE的长，又利用对角线互相平分的四边形是平行四边形，最后利用了平行四边形的面积公式．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
如图，在等腰△ABC中，直线l垂直底边BC，现将直线l沿线段BC从B点匀速平移至C点，直线l与△ABC的边相交于E、F两点．设线段EF的长度为y，平移时间为t，则下图中能较好反映y与t的函数关系的图象是（ ）
如图，△ABC中，点E、P在边AB上，且AE=BP，过点E、P作BC的平行线，分别交AC于点F、Q，记△AEF的面积为S1，四边形EFQP的面积为S2，四边形PQCB的面积为S3．
一个几何体由大小相同的小方块搭成，从上面看到的几何体的形状图如图所示，其中小正方形中的数字表示在该位置的小立方块的个数，则从正面看到几何体的形状图是（ ）
在直角坐标系中，直线y=x+1与y轴交于点A，按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C3C2…，A1、A2、A3…在直线y=x+1上，点C1、C2、C3…在x轴上，图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…Sn，则Sn的值为22n-3（用含n的代数式表示，n为正整数）．
如图，在⊙O中，AB为直径，OC⊥AB，弦CD与OB交于点F，在AB的延长线上有点E，且EF=ED．
