题目内容
20.∠ACB=60°,点O在∠ACB的平分线上,OC=5cm,以点O为圆心,3cm为半径作圆,则⊙O与AC的位置关系是相交.分析 如图,过点O作OH⊥AC于H,先计算出∴∠AOC=$\frac{1}{2}$∠AOB=30°,再利用含30度的直角三角形三边的关系得到OH=$\frac{1}{2}$OC=2.5,则点O到AC的距离小于圆的半径,然后根据直线与圆的位置关系的判定方法可判断直线AC与⊙O的位置关系.
解答 解:如图, 过点O作OH⊥AC于H,
过点O作OH⊥AC于H,
∵OC平分∠ACB
∴∠AOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×60°=30°,
在Rt△OHC中,OH=$\frac{1}{2}$OC=2.5,
∵⊙O的半径为3,
∴点O到AC的距离小于圆的半径,
∴直线AC与⊙O相交.
故答案为相交.
点评 本题考查了直线与圆的位置关系:设⊙O的半径为r,圆心O到直线l的距离为d:直线l和⊙O相交?d<r;直线l和⊙O相切?d=r直线l和⊙O相离?d>r.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
13. 如图,在平行四边形ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形(全等除外)有( )
如图,在平行四边形ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形(全等除外)有( )
 如图,在平行四边形ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形(全等除外)有( )
如图,在平行四边形ABCD中,BE交AC,CD于G,F,交AD的延长线于E,则图中的相似三角形(全等除外)有( )| A. | 3对 | B. | 4对 | C. | 5对 | D. | 6对 |
12.化简(2+1)(22+1)(24+1)(28+1)得( )
| A. | 28-1 | B. | 216+1 | C. | 216-1 | D. | 264-1 |
8.已知a-b=-2,那么-ax2+bx2化简的结果是( )
| A. | 2x2 | B. | -2x2 | C. | $\frac{1}{2}$x2 | D. | -$\frac{1}{2}$x2 |

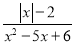 的值为0,则x的值为( )
的值为0,则x的值为( )